2022 AMC 8

Complete problem set with solutions and individual problem pages

Problem 12 Medium

The arrows on the two spinners shown below are spun. Let the number N equal 10 times the number on Spinner \text{A}, added to the number on Spinner \text{B}. What is the probability that N is a perfect square number?

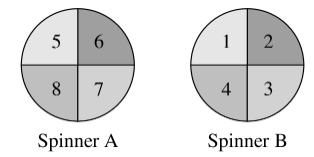
  • A.

    \dfrac{1}{16}

  • B.

    \dfrac{1}{8}

  • C.

    \dfrac{1}{4}

  • D.

    \dfrac{3}{8}

  • E.

    \dfrac{1}{2}

Answer:B

Solution 1

First, we calculate that there are a total of 4\cdot4=16 possibilities. Now, we list all of two-digit perfect squares. 64 and 81 are the only ones that can be made using the spinner. Consequently, there is a \frac{2}{16}=\boxed{\textbf{(B) }\dfrac{1}{8}} probability that the number formed by the two spinners is a perfect square.

 

Solution 2

There are 4 \cdot 4 = 16 total possibilities of N. We know N=10A+B, which A is a number from spinner A, and B is a number from spinner B. Also, notice that there are no perfect squares in the 50s or 70s, so only 4-2=2 values of N work, namely 64 and 81. Hence, \frac{2}{16}=\boxed{\textbf{(B) }\dfrac{1}{8}}.

Related Problems
Problem 10 2022 AMC 8
Problem 11 2022 AMC 8
Problem 13 2022 AMC 8
Problem 14 2022 AMC 8
Think Academy Powered by ChatGPT