2018 AMC 8
Complete problem set with solutions and individual problem pages
Problem 20 Hard
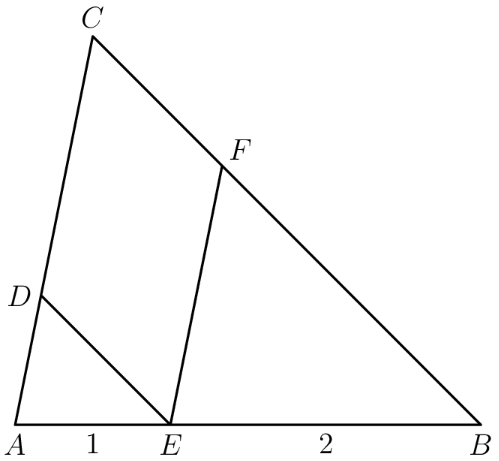
In a point is on with and Point is on so that and point is on so that What is the ratio of the area of to the area of
- A.
- B.
- C.
- D.
- E.
Answer:A
By similar triangles, we have . Similarly, we see that . Using this information, we get
Then, since , it follows that the . Thus, the answer would be .
