2019 AMC 8
Complete problem set with solutions and individual problem pages
Quadrilateral is a rhombus with perimeter meters. The length of diagonal is meters. What is the area in square meters of rhombus ?

- A.
- B.
- C.
- D.
- E.
Solution 1
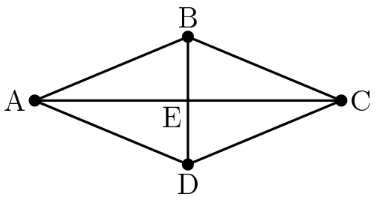
A rhombus has sides of equal length. Because the perimeter of the rhombus is , each side is . In a rhombus, diagonals are perpendicular and bisect each other, which means = = .
Consider one of the
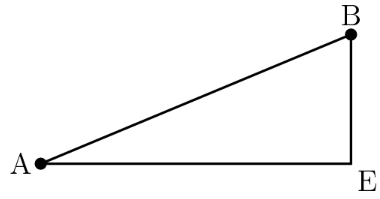
= , and = . Using the Pythagorean theorem, we find that = . You know the Pythagorean triple (5, 12, 13).
Thus the values of the two diagonals are = and = . The area of a rhombus is = = =
Solution 2
Right off the bat, we can see that the perimeter of the figure is 52. Dividing this by four, we can get that each side is equal to 13. By drawing a line perpendicular to the one given, we can split the figure into four right triangles. 12 (24/2) is equal to the height of one small right triangle, and 13 is the slanted side. Using the Pythagorean theorem we can find that 169 (13 squared) - 144 (12 squared) = 25 (five squared). With this, we can determine that each small right triangle equals 30. Multiplying that by four we can get
