2021 AMC 10 A Fall
Complete problem set with solutions and individual problem pages
Each of the edges of a cube is labeled or . Two labelings are considered different even if one can be obtained from the other by a sequence of one or more rotations and/or reflections. For how many such labelings is the sum of the labels on the edges of each of the faces of the cube equal to ?(2021 AMC Fall 10A, Question #24)
- A.
- B.
- C.
- D.
- E.
Solution 1:
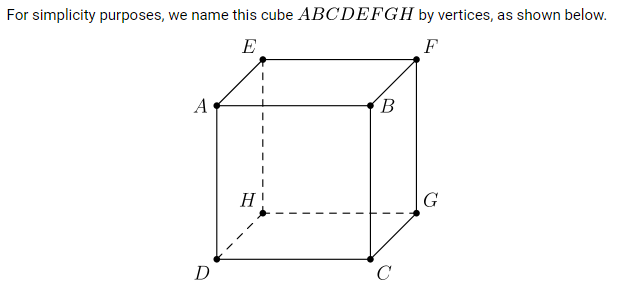
Note that for each face of this cube, two edges are labeled 0 and two edges are labeled 1 . For all twelve edges of this cube, we conclude that six edges are labeled 0 , and six edges are labeled
We apply casework to face . Recall that there are ways to label its edges:
1. Opposite edges have the same label. There are 2 ways to label the edges of . We will consider one of the ways, then multiply the count by 2 . Without the loss of generality, we assume that are labeled , respectively: We apply casework to the label of , as shown below.
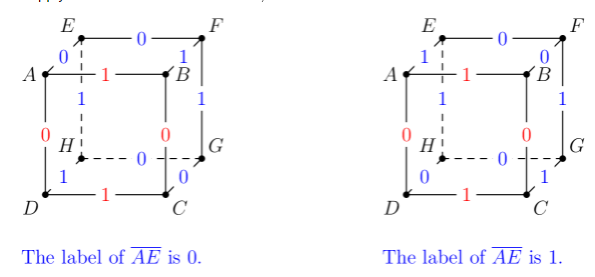
We have such labelings for this case.
2. Opposite edges have different labels. There are 4 ways to label the edges of . We will consider one of the ways, then multiply the count by 4 . Without the loss of generality, we assume that are labeled , respectively: We apply casework to the labels of and , as shown below.
We have such labelings for this case. Therefore, we have (E) 20 such labelings in total.
Solution 2:
Since we want the sum of the edges of each face to be , we need there to be two 1 s and two 0s on each face. Through experimentation, we find that either , or all of them have adjacent to and adjacent to on each face. WLOG, let the first face (counterclockwise) be . In this case we are trying to have all of them be adjacent to each other. First face: . Second face: choices: or . After that, it is basically forced and everything will fall in to place. Since we assumed WLOG, we need to multiply by to get a total of 8 different arrangements.
Secondly, 4 of the faces have all of them adjacent and of the faces do not: WLOG counting counterclockwise, we have . Then, we choose the other face next to it. There are two cases, which are and . Therefore, this subcase has 4 different arrangements. Then, we can choose the face at front to be . This has 4 cases. The sides can either be or . Therefore, we have another 8 cases. Summing these up, we have . Therefore, our answer is . Remark It is very easy to get disorganized when counting, so when doing this problem, make sure to draw a diagram of the cube. Labeling is a bit harder, since we often confuse one side with another. Try doing the problem by labeling sides on the lines (literally letting the lines pass through your and .) I found that to be very helpful when solving this problem.
