2022 AMC 8

Complete problem set with solutions and individual problem pages

Problem 25 Hard

A cricket randomly hops between 4 leaves, on each turn hopping to one of the other 3 leaves with equal probability. After 4 hops what is the probability that the cricket has returned to the leaf where it started?

  • A.

    \frac{2}{9}

  • B.

    \frac{19}{80}

  • C.

    \frac{20}{81}

  • D.

    \frac{1}{4}

  • E.

    \frac{7}{27}

Answer:E

Solution 1 (Casework)

Let A denote the leaf where the cricket starts and B denote one of the other 3 leaves. Note that:

- If the cricket is at A, then the probability that it hops to B next is 1.

- If the cricket is at B, then the probability that it hops to A next is \frac13.

- If the cricket is at B, then the probability that it hops to B next is \frac23.

We apply casework to the possible paths of the cricket:

1. A \rightarrow B \rightarrow A \rightarrow B \rightarrow A

~~~The probability for this case is 1\cdot\frac13\cdot1\cdot\frac13=\frac19.

2. A \rightarrow B \rightarrow B \rightarrow B \rightarrow A

~~~The probability for this case is 1\cdot\frac23\cdot\frac23\cdot\frac13=\frac{4}{27}.

Together, the probability that the cricket returns to A after 4 hops is \frac19+\frac{4}{27}=\boxed{\textbf{(E) }\frac{7}{27}}.

 

Solution 2 (Casework)

We can label the leaves as shown below:

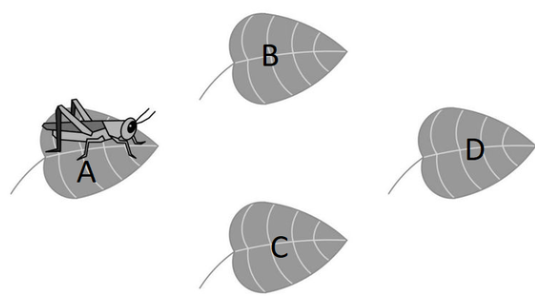
Carefully counting cases, we see that there are 7 ways for the cricket to return to leaf A after four hops if its first hop was to leaf B:

1. A \rightarrow B \rightarrow A \rightarrow B \rightarrow A

2. A \rightarrow B \rightarrow A \rightarrow C \rightarrow A

3. A \rightarrow B \rightarrow A \rightarrow D \rightarrow A

4. A \rightarrow B \rightarrow C \rightarrow B \rightarrow A

5. A \rightarrow B \rightarrow C \rightarrow D \rightarrow A

6. A \rightarrow B \rightarrow D \rightarrow B \rightarrow A

7. A \rightarrow B \rightarrow D \rightarrow C \rightarrow A

By symmetry, we know that there are 7 ways if the cricket's first hop was to leaf C, and there are 7 ways if the cricket's first hop was to leaf D. So, there are 21 ways in total for the cricket to return to leaf A after four hops.

Since there are 3^4 = 81 possible ways altogether for the cricket to hop to any other leaf four times, the answer is \frac{21}{81} = \boxed{\textbf{(E) }\frac{7}{27}}.

Related Problems
Problem 21 2022 AMC 8
Problem 22 2022 AMC 8
Problem 23 2022 AMC 8
Problem 24 2022 AMC 8
Think Academy Powered by ChatGPT