2022 AMC 10 A

Complete problem set with solutions and individual problem pages

Problem 10 Easy

Daniel finds a rectangular index card and measures its diagonal to be 8 centimeters. Daniel then cuts out equal squares of side 1cm at two opposite cormers of the index card and measures the distance between the two closest vertices of these squares to be 4\sqrt{2}  centimeters, as shown below. What is the area of the original index card?

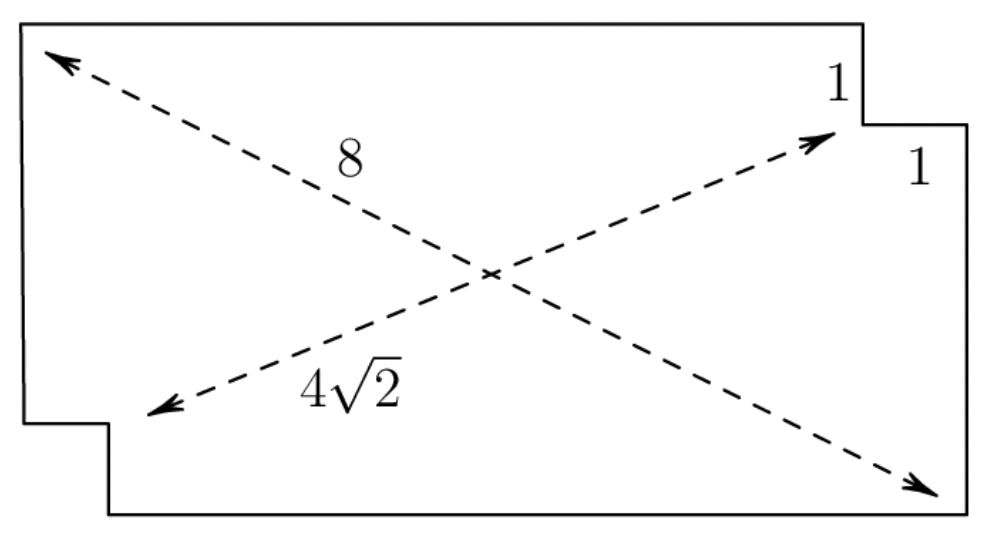
  • A.

    14

  • B.

    10\sqrt{2}

  • C.

    16

  • D.

    12\sqrt{2}

  • E.

    18

Answer:E

Assume the length of the index is x and the width is y.

x^2+y^2=8^2=64

(x-2)^2+(y-2)^2=(4\sqrt{2})^2=32

x^2-4x+4+y^2-4y+4=32

(x^2+y^2)-4(x+y)=24

4(x+y)=40

x+y=10

(x+y)^2=x^2+y^2+2xy=100

2xy=100-64=36

Area =xy=18

Related Problems
Problem 8 2022 AMC 10 A
Problem 9 2022 AMC 10 A
Problem 11 2022 AMC 10 A
Problem 12 2022 AMC 10 A
Think Academy Powered by ChatGPT