2014 AMC 8

Complete problem set with solutions and individual problem pages

Problem 15 Medium

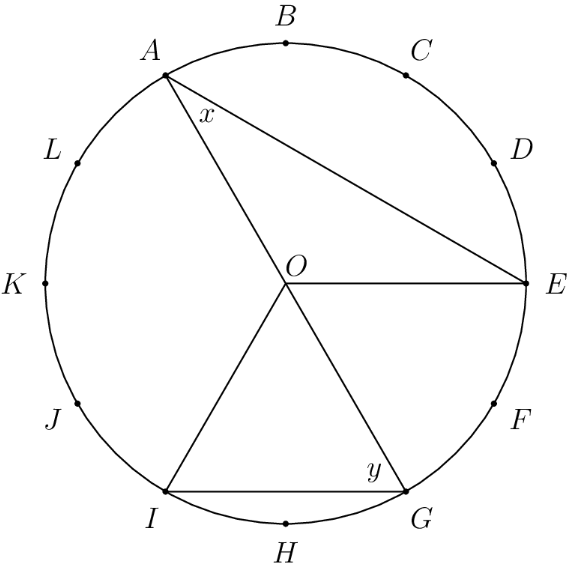
The circumference of the circle with center O is divided into 12 equal arcs, marked the letters A through L as seen below. What is the number of degrees in the sum of the angles x and y?

  • A.

    75

  • B.

    80

  • C.

    90

  • D.

    120

  • E.

    150

Answer:C

Solution 1

The measure of an inscribed angle is half the measure of its corresponding central angle. Since each unit arc is \frac{1}{12} of the circle's circumference, each unit central angle measures \frac{360}{12}^{\circ}=30^{\circ}. From this, \angle EOG = 60^{\circ}, so x = 30^{\circ}. Also, \angle AOI = 120^{\circ}, so y = 60^{\circ}. The number of degrees in the sum of both angles is 30 + 60 = \boxed{(C)\ 90}.

 

Solution 2

Since \triangle AOE is isosceles and \angle AOE = \frac{4}{12} \cdot 360^{\circ} = 120^{\circ}, x = 30^{\circ}. Since \triangle GOI is isosceles and \angle GOI = \frac{2}{12} \cdot 360^{\circ} = 60^{\circ}, x = 60^{\circ}. The number of degrees in the sum of both angles is 30+60 = \boxed{(C)\ 90}.

Related Problems
Problem 13 2014 AMC 8
Problem 14 2014 AMC 8
Problem 16 2014 AMC 8
Problem 17 2014 AMC 8
Think Academy Powered by ChatGPT