2016 AMC 8
Complete problem set with solutions and individual problem pages
Problem 2 Easy
In rectangle , and . Point is the midpoint of . What is the area of ?
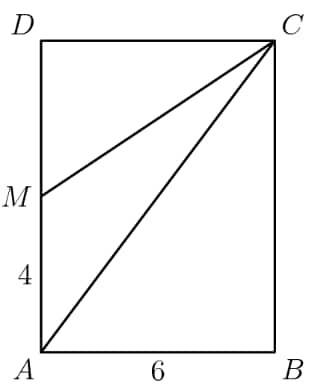
- A.
- B.
- C.
- D.
- E.
Answer:A
Solution 1
Using the triangle area formula for triangles: where is the area, is the base, and is the height. This equation gives us .
Solution 2
A triangle with the same height and base as a rectangle is half of the rectangle's area. This means that a triangle with half of the base of the rectangle and also the same height means its area is one quarter of the rectangle's area. Therefore, we get .
