AMC 10 Daily Practice Round 3

Complete problem set with solutions and individual problem pages

Problem 15 Medium

A rectangle with dimensions 100 \text{ cm} by 150 \text{ cm} is tilted so that one corner is 20 \text{ cm} above a horizontal line, as shown. To the nearest centimeter, determine the height of vertex Z above the horizontal line.

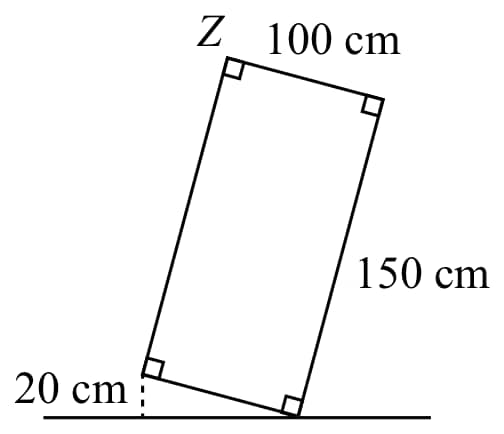
  • A.

    164

  • B.

    165

  • C.

    166

  • D.

    167

  • E.

    168

Answer:D

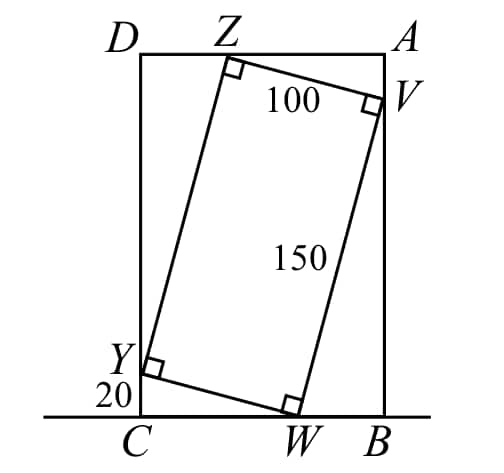
Since V W Y Z is a rectangle, then Y W=Z V=100 and Z Y=V W=150. Since \triangle Y C W is right-angled at C, by the Pythagorean Theorem,

C W^2=Y W^2-Y C^2=100^2-20^2=10000-400=9600

Since C W>0, then C W=\sqrt{9600}=\sqrt{1600 \cdot 6}=\sqrt{1600} \cdot \sqrt{6}=40 \sqrt{6}. The height of Z above the horizontal line is equal to the length of D C, which equals D Y+Y C which equals D Y+20. Now \triangle Z D Y is right-angled at D and \triangle Y C W is right-angled at C. Also, by Triple Perpendicular Model, \triangle Z D Y is similar to \triangle Y C W.

Therefore, \frac{D Y}{Z Y}=\frac{C W}{Y W} and so D Y=\frac{Z Y \cdot C W}{Y W}=\frac{150 \cdot 40 \sqrt{6}}{100}=60 \sqrt{6}. Finally, D C=D Y+20=60 \sqrt{6}+20 \approx 166.97. Rounded to the nearest integer, D C is 167.

Related Problems
Problem 13 AMC 10 Daily Practice Round 3
Problem 14 AMC 10 Daily Practice Round 3
Problem 16 AMC 10 Daily Practice Round 3
Problem 17 AMC 10 Daily Practice Round 3
Think Academy Powered by ChatGPT