2024 AMC 8
Complete problem set with solutions and individual problem pages
Problem 20 Hard
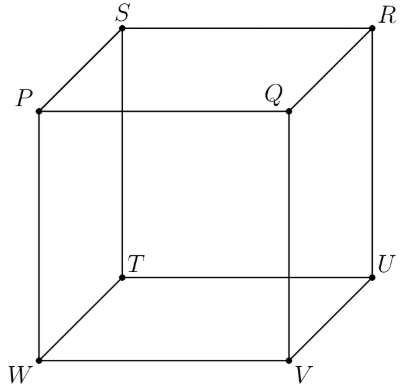
Any three vertices of the cube , shown in the figure below, can be connected to form a triangle. (For example, vertices , , and can be connected to form isosceles .) How many of these triangles are equilateral and contain as a vertex?
- A.
- B.
- C.
- D.
- E.
Answer:D
Solution 1
The only equilateral triangles that can be formed are through the diagonals of the faces of the square. From P you have possible vertices that are possible to form a diagonal through one of the faces. Therefore, there are possible triangles. So the answer is .
Solution 2
Each other compatible point must be an even number of edges away from P, so the compatible points are R, V, and T. Therefore, we must choose two of the three points, because P must be a point in the triangle. So, the answer is .
Think Academy Powered by ChatGPT