2024 AMC 8
Complete problem set with solutions and individual problem pages
Jean has made a piece of stained glass art in the shape of two mountains, as shown in the figure below. One mountain peak is feet high while the other peak is feet high. Each peak forms a angle, and the straight sides form a angle with the ground. The artwork has an area of square feet. The sides of the mountain meet at an intersection point near the center of the artwork, feet above the ground. What is the value of
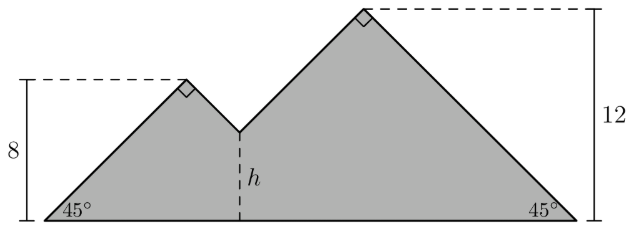
- A.
- B.
- C.
- D.
- E.
Extend the "inner part" of the mountain so that the image is two right triangles that overlap in a third right triangle as shown.
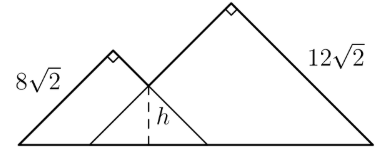
The side length of the largest right triangle is which means its area is Similarly, the area of the second largest right triangle is (the side length is ), and the area of the overlap is (the side length is ). Because the right triangles have a side ratio of 1:1:.Thus,
which means that the answer is
