AMC 10 Daily Practice - Similarity

Complete problem set with solutions and individual problem pages

Problem 2 Easy

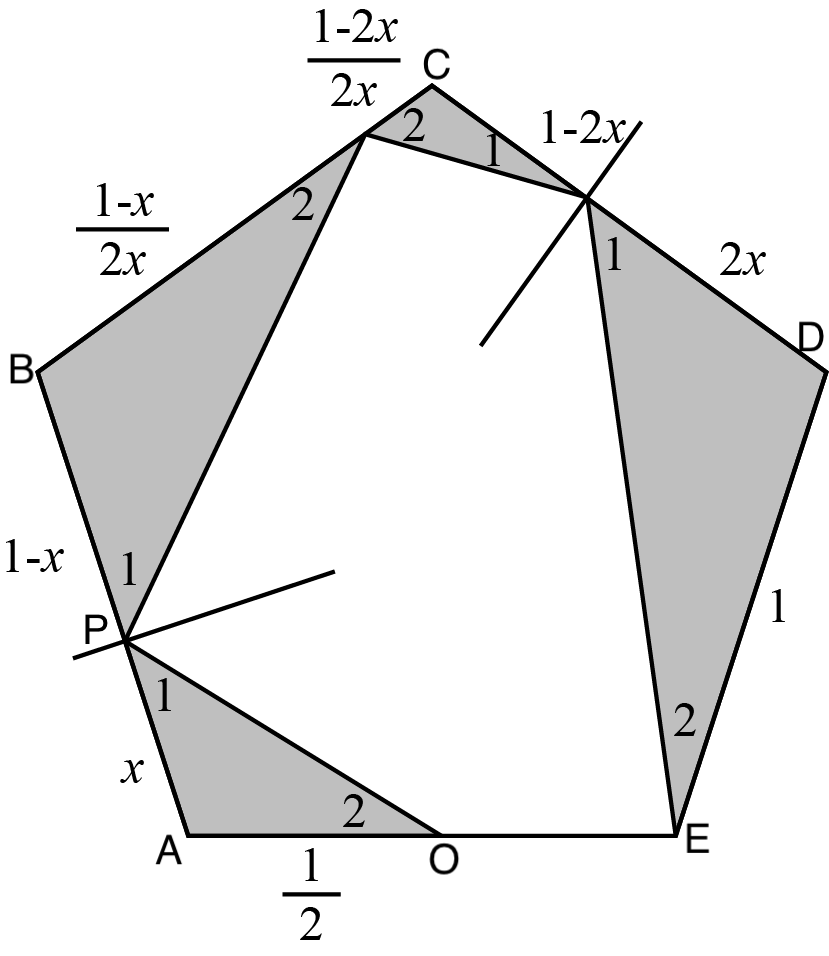
In a new billiard game, the table is a regular pentagon ABCDE with side length 1 meter. The five vertices are pockets. The ball is always struck from the midpoint O of AE. When the ball hits the edge of the table, it rebounds. If the ball reaches a pocket, it falls in. After a shot, the ball first hits point P on edge AB, then rebounds towards edge \overline{BC}, rebounds again at edge \overline{BC}, then rebounds at edge \overline{CD}, and finally falls into pocket E. What is the distance between point P and point A?

​​​

  • A.

    \frac{1}{5}

  • B.

    \frac{1}{6}

  • C.

    \frac{2}{5}

  • D.

    \frac{3}{4}

  • E.

    \frac{5}{2}

Answer:C

By symmetry, we know all \angle 1 are equal and all \angle 2 are equal. So the triangles are all similar.

\frac{1-2x}{2x} + \frac{1-x}{2x} = 1

2 - 3x = 2x

x = \frac{2}{5}

Related Problems
Problem 1 AMC 10 Daily Practice - Similarity
Problem 3 AMC 10 Daily Practice - Similarity
Think Academy Powered by ChatGPT