2025 AMC 8
Complete problem set with solutions and individual problem pages
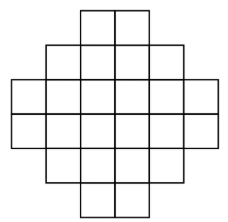
Problem 12 Medium
The region shown below consists of 24 squares, each with side length 1 centimeter. What is the area, in square centimeters, of the largest circle that can fit inside the region, possibly touching the boundaries?
- A.
- B.
- C.
- D.
- E.
Answer:C
Solution 1
The largest circle that can fit inside the figure has its center in the middle of the figure and will be tangent to the figure in points. By the Pythagorean Theorem, the distance from the center to one of these points is , so the area of this circle is .
Solution 2
Draw the circle in the grid and analyze the radius. Its radius is a little more than 2 but a lot less than 2.5, so the area is a little more than . So, the area of the circle is with a radius of approximately 2.23.
