AMC 8 Daily Practice - Circles

Complete problem set with solutions and individual problem pages

Problem 2 Easy

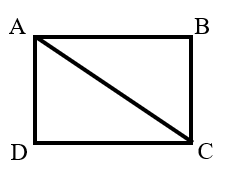
As shown in the figure, ABCD is a rectangle with length 4, width 3, and diagonal length 5. It is rotated 90^\circ clockwise around point C. Find the area swept by side AB.(Take \pi=3.14)

  • A.

    7.065

  • B.

    9.42

  • C.

    12.56

  • D.

    15.7

  • E.

    19.625

Answer:C

The area swept by side AB is the area of the shaded part in the figure.

The area swept by AB = (\text{Area of sector } ACA' + \text{Area of } \triangle A'B'C) -(\text{Area of sector } BCB' + \text{the area of } \triangle ABC).

Since the area of \triangle ABC is equal to the area of \triangle A'B'C, this simplifies to: \text{Area of sector } ACA' - \text{Area of sector } BCB'.

Calculating the areas of the sectors :

= \pi \times 5^2 \times \frac{1}{4} - \pi \times 3^2 \times \frac{1}{4}

= \pi \times 25 \times \frac{1}{4} - \pi \times 9 \times \frac{1}{4}

= \pi \times (25 - 9) \times \frac{1}{4} = \pi \times 16 \times \frac{1}{4}

= 4\pi = 12.56 \quad (\text{taking } \pi \approx 3.14)

Answer: The areas swept by sides AB is 12.56 square units.

Related Problems
Problem 1 AMC 8 Daily Practice - Circles
Problem 3 AMC 8 Daily Practice - Circles
Problem 4 AMC 8 Daily Practice - Circles
Problem 5 AMC 8 Daily Practice - Circles
Think Academy Powered by ChatGPT