2024 AMC 8
Complete problem set with solutions and individual problem pages
Problem 11 Medium
The coordinates of are , , and , with . The area of is 12. What is the value of ?
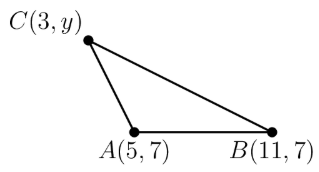
- A.
- B.
- C.
- D.
- E.
Answer:D
Solution 1
Since the triangle has a base of , we can plug in that value as the base. Then, we can solve the equation for the height. Doing so gives us,
This means that , so that means that we have to add 4 to the -coordinate. So the answer is
Solution 2
By the Shoelace Theorem, has area
From the problem, this is equal to . We now solve for y.
OR
OR
OR
However, since, as stated in the problem, , our only valid solution is .
