2017 AMC 8

Complete problem set with solutions and individual problem pages

Problem 25 Hard

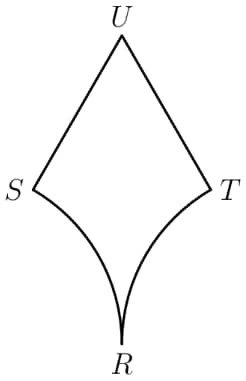
In the figure shown, \overline{US} and \overline{UT} are line segments each of length 2, and m\angle TUS = 60^\circ. Arcs \widehat{TR} and \widehat{SR} are each one-sixth of a circle with radius 2. What is the area of the region shown?

  • A.

    3 \sqrt{3}-\pi

  • B.

    4\sqrt{3} - \frac{4 \pi}{3}

  • C.

    2\sqrt{3}

  • D.

    4\sqrt{3}-\frac{2\pi}{3}

  • E.

    4+\frac{4\pi}{3}

Answer:B

Solution 1

In addition to the given diagram, we can draw lines \overline{SR} and \overline{RT}. The area of rhombus SRTU is half the product of its diagonals, which is \frac{2\sqrt3 \cdot 2}{2}=2\sqrt3. However, we have to subtract off the circular segments. The area of those can be found by computing the area of the circle with radius 2, multiplying it by \frac{1}{6}, then finally subtracting the area of an equilateral triangle with a side length 2 from the sector. The sum of the areas of the circular segments is 2(\frac{4 \pi}{6}-\sqrt3). The area of rhombus SRTU minus the circular segments is 2\sqrt3-\frac{4 \pi}{3}+2\sqrt3= \boxed{\textbf{(B)}\ 4\sqrt{3}-\frac{4\pi}{3}}.

 

Solution 2

We can extend \overline{US}, \overline{UT} to X and Y, respectively, such that X and Y are collinear to point R. Connect \overline{XY}. We can see points X, Y are probably circle centers of arc SR, TR, respectively. So, \overline{XS} = 2 = \overline{TY}. Thus, \triangle{UXY} is equilateral. The area of \triangle{UXY} is \frac{\sqrt{3}}{4} \cdot 4^2, or 4\sqrt{3}, and both one sixth circles total up to \frac{4\pi}{3}. Finally, the answer is \boxed{\textbf{(B)} 4\sqrt{3}-\frac{4\pi}{3}}.

Related Problems
Problem 21 2017 AMC 8
Problem 22 2017 AMC 8
Problem 23 2017 AMC 8
Problem 24 2017 AMC 8
Think Academy Powered by ChatGPT