2025 AMC 10 A
Complete problem set with solutions and individual problem pages
Problem 6 Easy
In an equilateral triangle each interior angle is trisected by a pair of rays. The intersection of the interiors of the middle -angle at each vertex is the interior of a convex hexagon. What is the degree measure of the smallest angle of this hexagon?
- A.
- B.
- C.
- D.
- E.
Answer:C
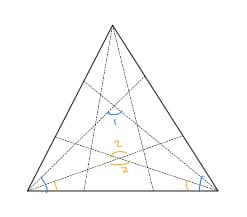
Computing the angles:
By symmetry, the hexagon's six angles are .
