2025 AMC 10 A

Complete problem set with solutions and individual problem pages

Problem 14 Easy

Six chairs are arranged around a round table. Two students and two teachers randomly select four of the chairs to sit in. What is the probability that the two students will sit in two adjacent chairs and the two teachers will also sit in two adjacent chairs?

  • A.

    \frac { 1 } { 6 }

  • B.

    \frac { 1 } { 5 }

  • C.

    \frac { 2 } { 9 }

  • D.

    \frac { 3 } { 1 3 }

  • E.

    \frac { 1 } { 4 }

Answer:B

 

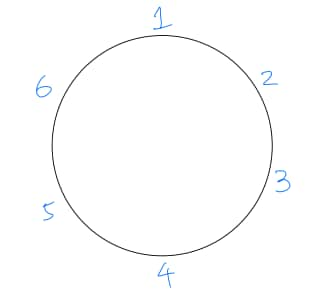
We may label the six seats as 1,2,3,4,5,6 on a round table.

Choose the two seats for the two students (order of the two students does not matter).

There are \binom{6}{2} unordered choices in total, while the adjacent pairs are (1,2),(2,3),(3,4),(4,5),(5,6),(6,1), hence 6 choices. Therefore P(\text{adjacent\ students}) = \frac{6}{\binom{6}{2}} = \frac{2}{5}

Given that the students are adjacent, without loss of generality, suppose they occupy seats (1,2). The remaining seats are \{3,4,5,6\}. Among these four, the adjacent pairs (on the circle) are (3,4), (4,5), (5,6), so there are 3 favorable pairs for the two teachers out of \binom{4}{2} unordered choices. Thus P(\text{adjacent\ teachers} \mid \text{adjacent\ students}) = \frac{3}{\binom{4}{2}}=\frac{1}{2}

Thus the final answer is P(\text{adjacent\ students}) \cdot P(\text{adjacent\ teachers} \mid \text{adjacent\ students}) = \frac{2}{5}\cdot \frac{1}{2} = \frac{1}{5}

Related Problems
Problem 12 2025 AMC 10 A
Problem 13 2025 AMC 10 A
Problem 15 2025 AMC 10 A
Problem 16 2025 AMC 10 A
Think Academy Powered by ChatGPT