2022 AMC 10 B
Complete problem set with solutions and individual problem pages
Each square in a grid is either filled or empty, and has up to eight adjacent neighboring squares, where neighboring squares share either a side or a corner. The grid is transformed by the following rules:
-Any filled square with two or three filled neighbors remains filled.
-Any empty square with exactly three filled neighbors becomes a filled square.
-All other squares remain empty or become empty.
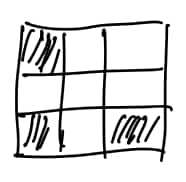
A sample transformation is shown in the figure below.
Suppose the grid has a border of empty squares surrounding a subgrid. How many initial configurations will lead to a transformed grid consisting of a single filled square in the center after a single transformation? (Rotations and reflections of the same configuration are considered different.)
- A.
- B.
- C.
- D.
- E.
This is actually a very famous mathematical game called "Conway's Game of Life", which is the most well-known two-dimensional cellular automaton. Its inventor, Professor John Horton Conway, passed away in 2020, and the question writer may have been paying tribute to him in this way.
After discussing the background, let's get back to the problem itself. We will discuss two cases:
The first case is when the central square is initially empty. Therefore, among the eight squares surrounding it, there must be exactly three that are filled.
Its three filled neighbours are all in the corner.
For this case, we have initial configurations.
Two of its three filled neighbours are in the corner.
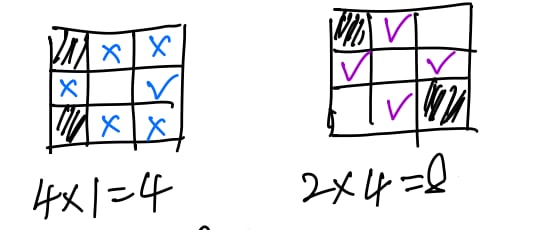
As shown in the diagram, we have initial configurations.
One of its three filled neighbours is in the corner.

As shown in the diagram, we have initial configurations.
None of its three filled neighbours is in the corner. At this point, there must be a filled square with two filled neighbours so that does not hold.
The second case is when the central square is initially filled. Therefore, among the eight squares surrounding it, there must be two or three that are filled.
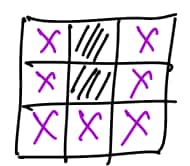
If one of it is not in the corner, then no matter how the other square is placed, there will always be a new filled point generated.
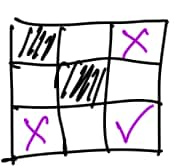
So all points must be in the corners, and at this point, there can only be two filled points and they must be placed in opposite corners. We have initial configurations.
So in total, we have initial configurations.
