2023 AMC 8

Complete problem set with solutions and individual problem pages

Problem 23 Hard

Each square in a 3 \times 3 grid is randomly filled with one of the 4 gray and white tiles shown below on the right.

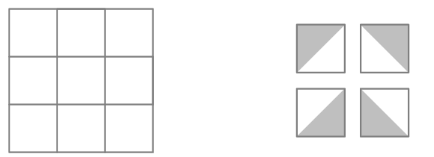
What is the probability that the tiling will contain a large gray diamond in one of the smaller 2 \times 2 grids? Below is an example of such tiling.

  • A.

    \frac{1}{1024}

  • B.

    \frac{1}{256}

  • C.

    \frac{1}{64}

  • D.

    \frac{1}{16}

  • E.

    \frac{1}{4}

Answer:C

Solution 1

There are 4 cases that the tiling will contain a large gray diamond in one of the smaller 2 \times 2 grids, as shown below:

There are 4^5 ways to decide the 5 white squares for each case, and the cases do not have any overlap.

So, the requested probability is

\frac{4\cdot4^5}{4^9} = \frac{4^6}{4^9} = \frac{1}{4^3} = \boxed{\textbf{(C) } \frac{1}{64}}.

 

Solution 2

Note that the middle tile can be any of the four tiles. The gray part of the middle tile points towards one of the corners, and for the gray diamond to appear the three adjacent tiles must all be perfect. Thus, the solution is \frac14 \cdot \frac14 \cdot \frac14 = \boxed{\textbf{(C) } \frac{1}{64}}.

Related Problems
Problem 21 2023 AMC 8
Problem 22 2023 AMC 8
Problem 24 2023 AMC 8
Problem 25 2023 AMC 8
Think Academy Powered by ChatGPT