AMC 8 Daily Practice - Triangle Properties

Complete problem set with solutions and individual problem pages

Problem 4 Easy

In triangle ABC, \angle B = 65^\circ. If \angle B is cut off along the dashed line, what is the sum of \angle ADE and \angle CED?

  • A.

    220^\circ

  • B.

    235^\circ

  • C.

    245^\circ

  • D.

    255^\circ

  • E.

    260^\circ

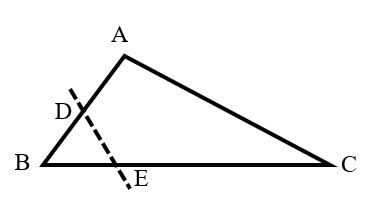
Answer:C

We know that: \angle ADE = \angle BDE + \angle B, \angle CED = \angle DEB + \angle B.

Then, the sum of \angle ADE and \angle CED is: \angle ADE + \angle CED = (\angle BDE + \angle B) + (\angle DEB + \angle B) = \angle BDE + \angle DEB + \angle B + \angle B.

In \triangle BDE, \angle BDE + \angle DEB + \angle B = 180^\circ.

Substituting this in, we get: \angle ADE + \angle CED = 180^\circ + \angle B

Since \angle B = 65^\circ: \angle ADE + \angle CED = 180^\circ + 65^\circ = 245^\circ.

Related Problems
Problem 2 AMC 8 Daily Practice - Triangle Properties
Problem 3 AMC 8 Daily Practice - Triangle Properties
Problem 5 AMC 8 Daily Practice - Triangle Properties
Problem 6 AMC 8 Daily Practice - Triangle Properties
Think Academy Powered by ChatGPT