2022 AMC 10 A

Complete problem set with solutions and individual problem pages

Problem 25 Easy

Let R, S, and T be squares that have vertices at lattice points (i.e. points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the x-axis. The left edge of R and the right edge of S are on the y-axis, and R contains as many lattice points as does S. The top two vertices of T are in R\cup S, and T contains \dfrac{1}{4} of the lattice points contained in R\cup S. See the figure (not drawn to scale).

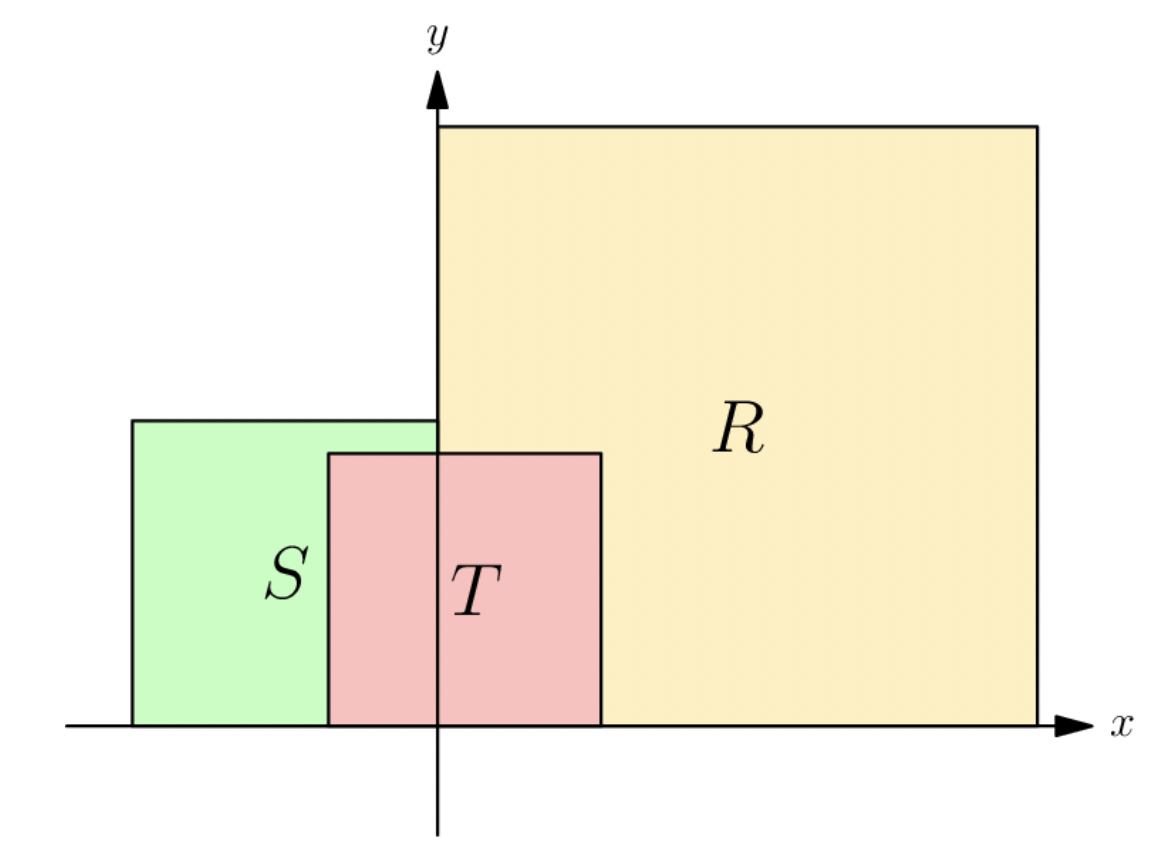
The fraction of lattice points in S that are in S\cap T is 27 times the fraction of lattice points in R that are in R\cap T. What is the minimum possible value of the edge length of R plus the edge length of S plus the edge length of T?

  • A.

    336

  • B.

    337

  • C.

    338

  • D.

    339

  • E.

    340

Answer:B

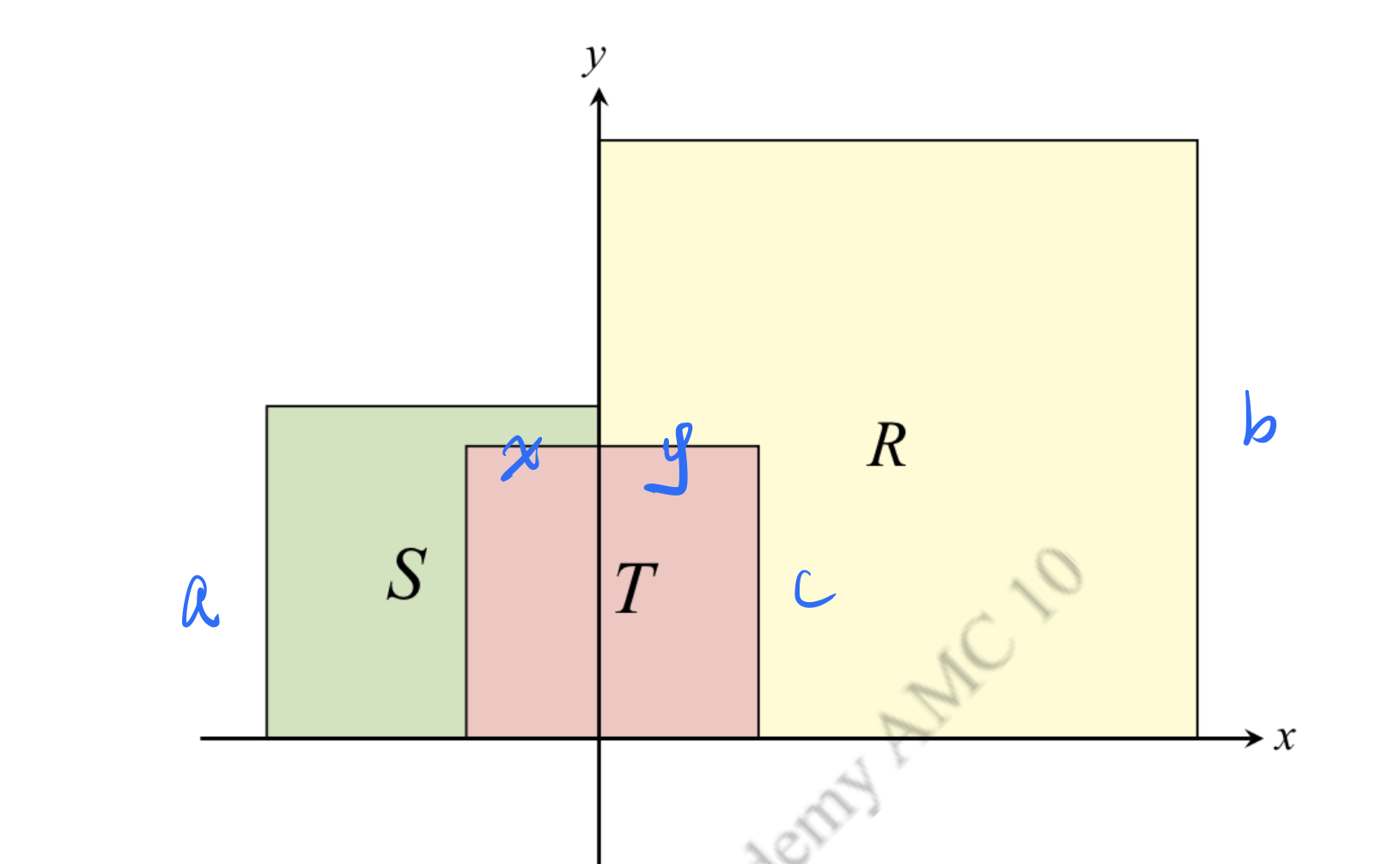
① \frac94 (a+1)^2=(b+1)^2

② S\cup R= (a+1)^2+(b+1)^2-(a+1)

T=\frac14 S\cup R=\frac14[(a+1)^2+(b+1)^2-(a+1)]

=\frac14[(a+1)^2+\frac94(a+1)^2-(a+1)]

=\frac{1}{16}(a+1)(13a+9)

=(c+1)^2

③ T\cap S=(x+1)(c+1)

T\cap R=(y+1)(c+1)

\frac{(x+1)(c+1)}{(b+1)^2}=27 \times \frac{(y+1)(c+1)}{(a+1)^2}

Then x+1=27 \times \frac 49 (y+1)=12(y+1)

c=x+y=13y+11

y=1\cdot 2\cdot3\cdot5\cdot5\cdot6\dots

When y=6, c=89.

The equation: \frac{1}{16}(a+1)(13a+9)=(c+1)^2) has integer solution.

a=99, b=149, so (a+b+c)_{min}=89+99+149=337.

Related Problems
Problem 21 2022 AMC 10 A
Problem 22 2022 AMC 10 A
Problem 23 2022 AMC 10 A
Problem 24 2022 AMC 10 A
Think Academy Powered by ChatGPT