AMC 8 Daily Practice - Circles
Complete problem set with solutions and individual problem pages
Problem 6 Easy
As shown in the figure, quadrilateral is inscribed in circle , , is the midpoint of arc , and . What is the measure of ?
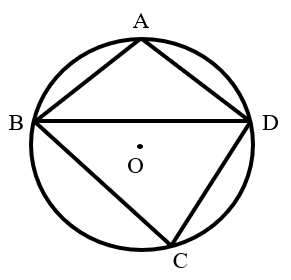
- A.
- B.
- C.
- D.
- E.
Answer:B
Connect , , , and .
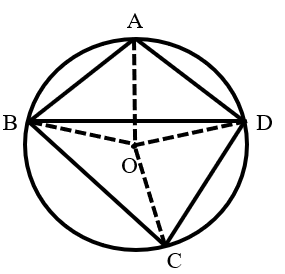
Since , the arcs they subtend are equal, so arc .
Because is the midpoint of arc , arc .
Therefore, arc .
is a circumferential angle subtended by arc , and .
The central angle subtended by the same arc is twice the circumferential angle, so .
The total degree measure of the circle is , so the sum of the central angles subtended by arcs , , and is: .
Since arc , their corresponding central angles are equal: .
is a circumferential angle subtended by arc , so it is half of the central angle : .
