2024 AMC 8
Complete problem set with solutions and individual problem pages
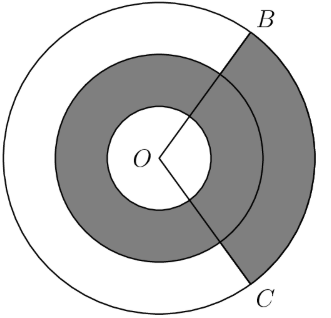
Three concentric circles centered at have radii of , , and . Points and lie on the largest circle. The region between the two smaller circles is shaded, as is the portion of the region between the two larger circles bounded by central angles , as shown in the figure below. Suppose the shaded and unshaded regions are equal in area. What is the measure of in degrees?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let .
We see that the shaded region is the inner ring plus a sector of the outer ring. Using the formula for the area of a circle (), we find that the area of is . This simplifies to .
The unshaded portion is comprised of the smallest circle plus the sector of the outer ring, which evaluates to .
We are told these are equal. Therefore, . Solving for reveals .
Solution 2
Notice that for the 3rd most outer ring of the circle, the ratio of the shaded region to non-shaded region is the ratio of to . With that, all we need to do is solve for the shaded region.
The inner most circle has radius , and the second circle has radius 2. Therefore, the first shaded area has area. The circle has total area , so the other shaded region must have area, as the non-shaded and shaded area is equivalent. So for the 3rd outer ring, the total area is , so the non-shaded part of the outer ring is .
Now as said before, the ratio of these two areas is the ratio of and . So, . We have where , , so our answer is .
