AMC 10 Daily Practice Round 3

Complete problem set with solutions and individual problem pages

Problem 5 Easy

The lines with equations y=mx+7, y=2, x=0, and y=0 form a trapezoid with area 3. If m>0, what is the value of m?

  • A.

    2

  • B.

    3

  • C.

    4

  • D.

    5

  • E.

    8

Answer:C

Let A and B be the points at which the line with equation y=mx+7 intersects the lines with equations y=0 and y=2, respectively. Also, suppose C has coordinates (0,2) and D has coordinates (0,0). The trapezoid in the problem is ABCD, as shown.

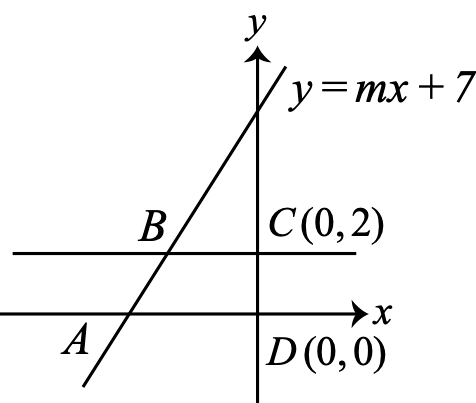
We can find the coordinates of A and B in terms of m. To find the coordinates of A, we find the point of intersection of the line with equation y=mx+7 and the line with equation y=0. Setting 0=mx+7, we get x=-\frac7m. Note that the y-coordinate of A must be 0 since it is, by definition, on the line with equation y=0. Therefore, the coordinates of A are (−\frac7m,0). Similarly, the coordinates of B are (−\frac5m,2). Trapezoid ABCD has parallel bases AD and BC and height CD. The two bases are horizontal and have lengths AD=\frac7m and BC=\frac5m. The length of CD is 2. Therefore, the area of ABCD is 12⋅CD⋅(AD+BC)=12⋅2⋅(\frac7m+\frac5m)=\frac{12}{m}. It is given that the area of the trapezoid is 3, so we have \frac{12}{m}=3, or m=4.

Related Problems
Problem 3 AMC 10 Daily Practice Round 3
Problem 4 AMC 10 Daily Practice Round 3
Problem 6 AMC 10 Daily Practice Round 3
Problem 7 AMC 10 Daily Practice Round 3
Think Academy Powered by ChatGPT