AMC 8 Daily Practice Round 11
Complete problem set with solutions and individual problem pages
Problem 14 Medium
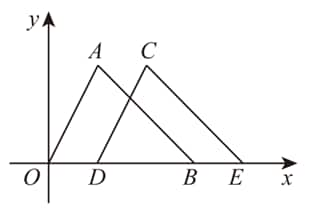
As shown in the figure, the coordinates of points and are and , respectively. The triangle is translated along the positive -axis so that point moves to point , forming the triangle . If , what are the coordinates of point ?
- A.
- B.
- C.
- D.
- E.
Answer:A
By analyzing the problem, we know that point satisfies . Since , we calculate . Therefore, is translated 1 unit to the right along the -axis to form . Point is also shifted 1 unit to the right, resulting in point having coordinates . Thus, the correct answer is .
