2023 AMC 8
Complete problem set with solutions and individual problem pages
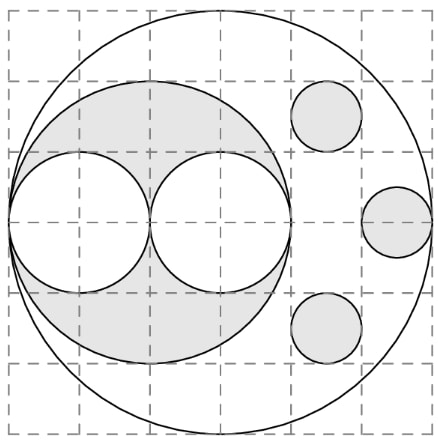
The figure below shows a large white circle with a number of smaller white and shaded circles in its interior. What fraction of the interior of the large white circle is shaded?
- A.
- B.
- C.
- D.
- E.
Solution 1
First, the total area of the radius circle is simply just when using our area of a circle formula.
Now from here, we have to find our shaded area. This can be done by adding the areas of the -radius circles and add; then, take the area of the radius circles and subtract that from the area of the radius circle to get our resulting complex shape area. Adding these up, we will get
.
So, our answer is .
Solution 2
Pretend each circle is a square. The large shaded circle is a square with area , and the two white circles inside it each have areas of , which adds up to . The three small shaded circles become three squares with area , and add up to . Adding the areas of the shaded circles (19) and subtracting the areas of the white circles (8), we get . Since the largest white circle in which all these other circles are becomes a square that has area , our answer is .
