AMC 10 Daily Practice Round 2
Complete problem set with solutions and individual problem pages
Circles , , and each have radius . Circles and share one point of tangency. Circle has a point of tangency with the midpoint of . One side of rectangle is tangent to both circles and , and its opposite side is tangent to circle . The other two sides are tangent to circles and , respectively. What is the area of the part that is inside the rectangle but not inside the circle?
- A.
- B.
- C.
- D.
- E.
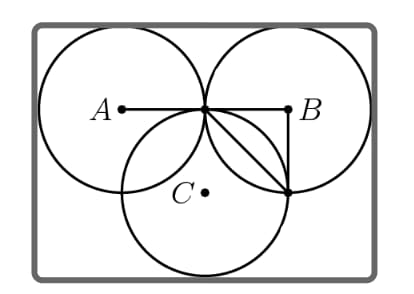
By the principle of inclusion-exclusion, it can be deduced that the desired area is equal to the area of the rectangle minus the sum of the areas of the three circles , and , plus the overlapping area between circle and circles and .
Then, we can compute the shaded area as the area of half of plus the area of the rectangle minus the area of the two sectors created by and . This is .
The area of the rectangle is , so the area is .
