2020 AMC 10 B
Complete problem set with solutions and individual problem pages
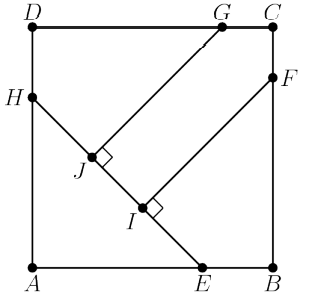
In square , points and lie on and , respectively, so that . Points and lie on and , respectively, and points and lie on so that and . See the figure below. Triangle , quadrilateral , quadrilateral , and pentagon each has area 1 . What is ?(2020 AMC 10B, Question #21)
- A.
- B.
- C.
- D.
- E.
Solution 1:
Since the total area is , the side length of square is 2 . We see that since triangle is a right isosceles triangle with area , we can determine sides and both to be . Now, consider extending and until they intersect. Let the point of intersection be . We note that is also a right isosceles triangle with side and find it's area to be . Now, we notice that is also a right isosceles triangle and find it's area to be . This is also equal to or . Since we are looking for , we want two times this. That gives(B)
Solution 2:
Since this is a geometry problem involving sides, and we know that is 2 , we can use our ruler and find the ratio between and . Measuring(on the booklet), we get that is about inches and is about inches. Thus, we can then multiply the length of by the ratio of , of which we then get . We take the square of that and of , and the closest answer to that is (B) . (Note that this is just a strategy I happened to use that worked. Do not press your luck with this strategy, for it was a lucky quess)
