2018 AMC 8
Complete problem set with solutions and individual problem pages
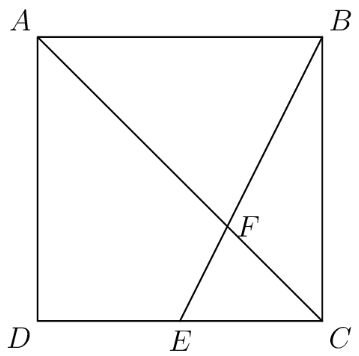
Point is the midpoint of side in square and meets diagonal at The area of quadrilateral is What is the area of
- A.
- B.
- C.
- D.
- E.
Solution 1
We can use analytic geometry for this problem.
Let us start by giving the coordinate , the coordinate , and so forth. and can be represented by the equations and , respectively. Solving for their intersection gives point coordinates .
Now, we can see that 's area is simply or . This means that pentagon 's area is of the entire square, and it follows that quadrilateral 's area is of the square.
The area of the square is then .
Solution 2
has half the area of the square. has base equal to half the square side length, and by AA Similarity with , it has the height, so has th of the area of square(). Thus, the area of the quadrilateral is of the area of the square. The area of the square is then .
