AMC 8 Daily Practice Round 7

Complete problem set with solutions and individual problem pages

Problem 30 Easy

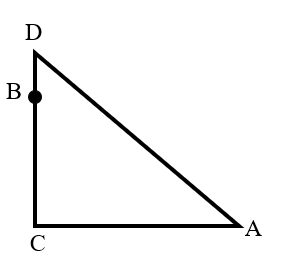
As shown in the figure, there are two monkeys at point B, which is 10 meters high on a tree. One monkey climbs down the tree to reach point A (a pond 20 meters away from the tree), and the other climbs to the top D of the tree and then jumps directly to A. The distance of the jump is calculated as a straight line. If the distances traveled by the two monkeys are equal, what is the height of the tree in meters?

  • A.

    15

  • B.

    16

  • C.

    17

  • D.

    18

  • E.

    19

Answer:A

Let DB = h.

In the right triangle DCA: DA = \sqrt{DC^2 + CA^2} = \sqrt{(h + 10)^2 + 20^2}.

Since the distances traveled by the two monkeys are equal:

DB + DA = BC + CA

h + \sqrt{(h + 10)^2 + 20^2} = 30

\sqrt{(h + 10)^2 + 20^2} = 30 - h

Solving this equation gives h = 5.

Thus, the height of the tree is 10 + 5 = 15 meters.

Related Problems
Problem 26 AMC 8 Daily Practice Round 7
Problem 27 AMC 8 Daily Practice Round 7
Problem 28 AMC 8 Daily Practice Round 7
Problem 29 AMC 8 Daily Practice Round 7
Think Academy Powered by ChatGPT