2020 AMC 8
Complete problem set with solutions and individual problem pages
Akash's birthday cake is in the form of a inch cube. The cake has icing on the top and the four side faces, and no icing on the bottom. Suppose the cake is cut into smaller cubes, each measuring inch, as shown below. How many of the small pieces will have icing on exactly two sides?

- A.
- B.
- C.
- D.
- E.
Solution 1
Notice that, for a small cube which does not form part of the bottom face, it will have exactly faces with icing on them only if it is one of the center cubes of an edge of the larger cube. There are such edges (as we exclude the edges of the bottom face), so this case yields small cubes. As for the bottom face, we can see that only the corner cubes have exactly faces with icing, so the total is .
Solution 2
The following diagram shows of the small cubes having exactly faces with icing on them; that is all of them except for those on the hidden face directly opposite the front face.
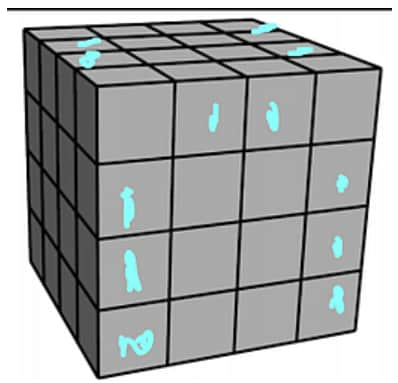
But the hidden face is an exact copy of the front face, so the answer is .
