AMC 8 Daily Practice - Circles

Complete problem set with solutions and individual problem pages

Problem 3 Easy

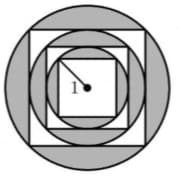
Some squares are inscribed in a set of concentric circles, as shown in the figure. Given that the radius of the smallest circle is 1cm, what is the area of the shaded part in square centimeters? (Take \pi = \frac{22}{7})

  • A.

    6

  • B.

    8

  • C.

    9

  • D.

    \frac{78}{7}

  • E.

    12

Answer:B

We calculate the area of the shaded part by dividing it into three parts:

the inner circle, the middle circle, and the outer circle.

the inner shaded area = the area of the inner circle - the area of the inner square:

\pi \times 1^2 - \left(\frac{2 \times 2}{2}\right) = \pi - 2 \quad (cm^{2})

The diameter of the inner circle is the side length of the middle square, which is 2cm. The diagonal of the middle square is the diameter of the middle circle.

Thus, the area of the middle shaded part is:

\pi \times \left(\frac{\sqrt{2^2 + 2^2}}{2}\right)^2 - (2 \times 2) = \pi \times 2 - 4 = 2\pi - 4 \quad (cm^{2}).

The area of the outer square is equal to the square of the diameter of the middle circle, which is 8cm^{2}. The square of the diagonal of the outer square is twice its area, so it is 16 cm², which equals the square of the diameter of the outer circle.

Thus, the area of the outer shaded part is:

\pi \times \left(\frac{\sqrt{16}}{2}\right)^2 - 8 = \pi \times 4 - 8 = 4\pi - 8 \quad (cm^{2})

Adding up the three parts, the total area of the shaded part is: (\pi - 2) + (2\pi - 4) + (4\pi - 8) = 7\pi - 14

Substituting \pi = \frac{22}{7}:

7 \times \frac{22}{7} - 14 = 22 - 14 = 8 \quad (cm^{2})

Answer: The area of the shaded part is 8cm^{2}.

Related Problems
Problem 1 AMC 8 Daily Practice - Circles
Problem 2 AMC 8 Daily Practice - Circles
Problem 4 AMC 8 Daily Practice - Circles
Problem 5 AMC 8 Daily Practice - Circles
Think Academy Powered by ChatGPT