AMC 10 Daily Practice Round 3
Complete problem set with solutions and individual problem pages
The diameter of a circle of radius is extended to a point outside the circle so that . Point is chosen so that and line is perpendicular to line . Segment intersects the circle at a point between and . What is the area of ?
- A.
- B.
- C.
- D.
- E.
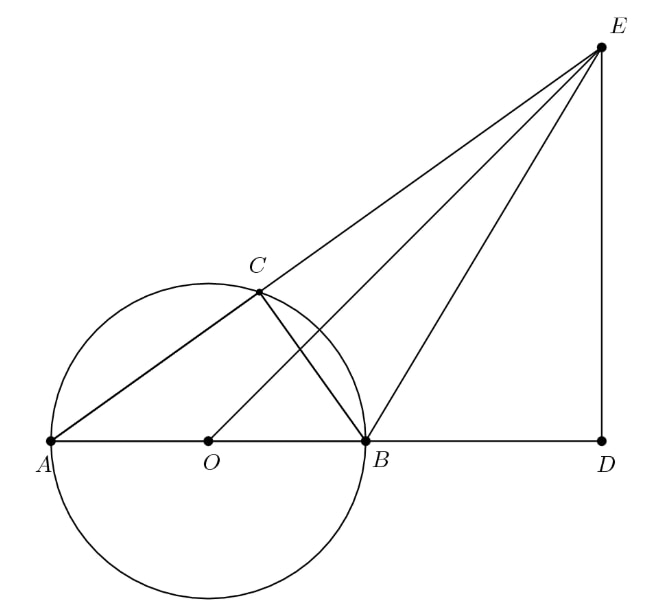
We note that by similarity. Also, since the area of and , , so the area of .
Let's call the center of the circle that segment is the diameter of . Note that is an isosceles right triangle. Solving for side , using the Pythagorean theorem, we find it to be . Calling the point where segment intersects circle , the point , segment would be . Also, noting that is a right triangle, we solve for side , using the Pythagorean Theorem, and get . Using Power of Point on point , we can solve for . We can subtract from to find and then solve for using Pythagorean theorem once more:
,
.
Now to solve for : ,
Note that is a right triangle because the hypotenuse is the diameter of the circle. Solving for area using the bases and , we get the area of triangle to be .
