2022 AMC 10 B

Complete problem set with solutions and individual problem pages

Problem 23 Hard

Ant Amelia starts on the number line at 0 and crawls in the following manner. For n=1,2,3, Amelia chooses a time duration t_{n} and an increment x_{n} independently and uniformly at random from the interval (0,1). During the nth step of the process, Amelia moves x_{n} units in the positive direction, using up t_{n} minutes. If the total elapsed time has exceeded 1 minute during the n^{\text{th}} step, she stops at the end of that step; otherwise, she continues with the next step, taking at most 3 steps in all. What is the probability that Amelia's position when she stops will be greater than 1?

  • A.

    \dfrac{1}{3}

  • B.

    \dfrac{1}{2}

  • C.

    \dfrac{2}{3}

  • D.

    \dfrac{3}{4}

  • E.

    \dfrac{5}{6}

Answer:C

Let x and y be random variables that are independently and uniformly distributed in the interval (0,1). Note that P(x+y \leq 1)=\frac{\frac{1}{2} \cdot 1^2}{1^2}=\frac{1}{2}, as shown below:

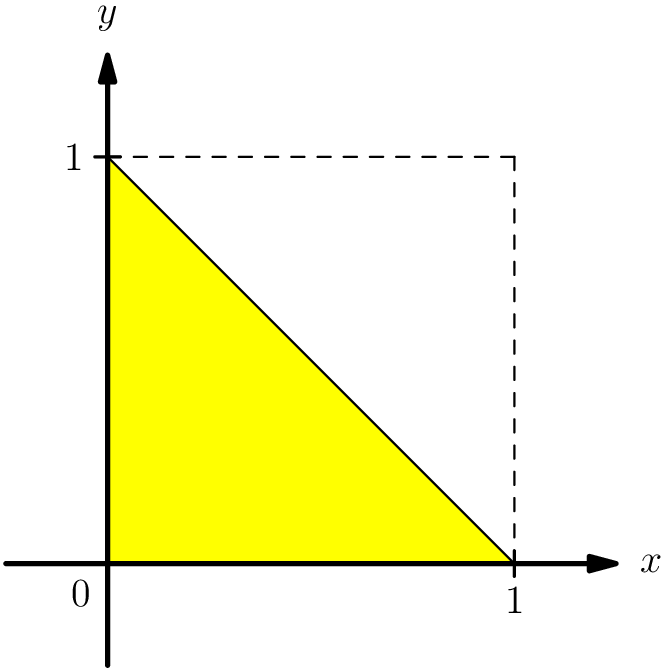
Let x, y, and z be random variables that are independently and uniformly distributed in the interval (0,1). Note that P(x+y+z \leq 1)=\frac{\frac{1}{3} \cdot\left(\frac{1}{2} \cdot 1^2\right) \cdot 1}{1^3}=\frac{1}{6}, as shown below:

We have two cases: 1. Amelia takes exactly 2 steps. We need x_1+x_2>1 and t_1+t_2>1. So, the probability is P\left(x_1+x_2>1\right) \cdot P\left(t_1+t_2>1\right)=\left(1-\frac{1}{2}\right) \cdot\left(1-\frac{1}{2}\right)=\frac{1}{4}.

2. Amelia takes exactly 3 steps. We need x_1+x_2+x_3>1 and t_1+t_2 \leq 1. So, the probability is P\left(x_1+x_2+x_3>1\right) \cdot P\left(t_1+t_2 \leq 1\right)=\left(1-\frac{1}{6}\right) \cdot \frac{1}{2}=\frac{5}{12} . Together, the answer is \frac{1}{4}+\frac{5}{12}= (C) \frac{2}{3}.

Related Problems
Problem 21 2022 AMC 10 B
Problem 22 2022 AMC 10 B
Problem 24 2022 AMC 10 B
Problem 25 2022 AMC 10 B
Think Academy Powered by ChatGPT