2025 AMC 10 A

Complete problem set with solutions and individual problem pages

Problem 15 Easy

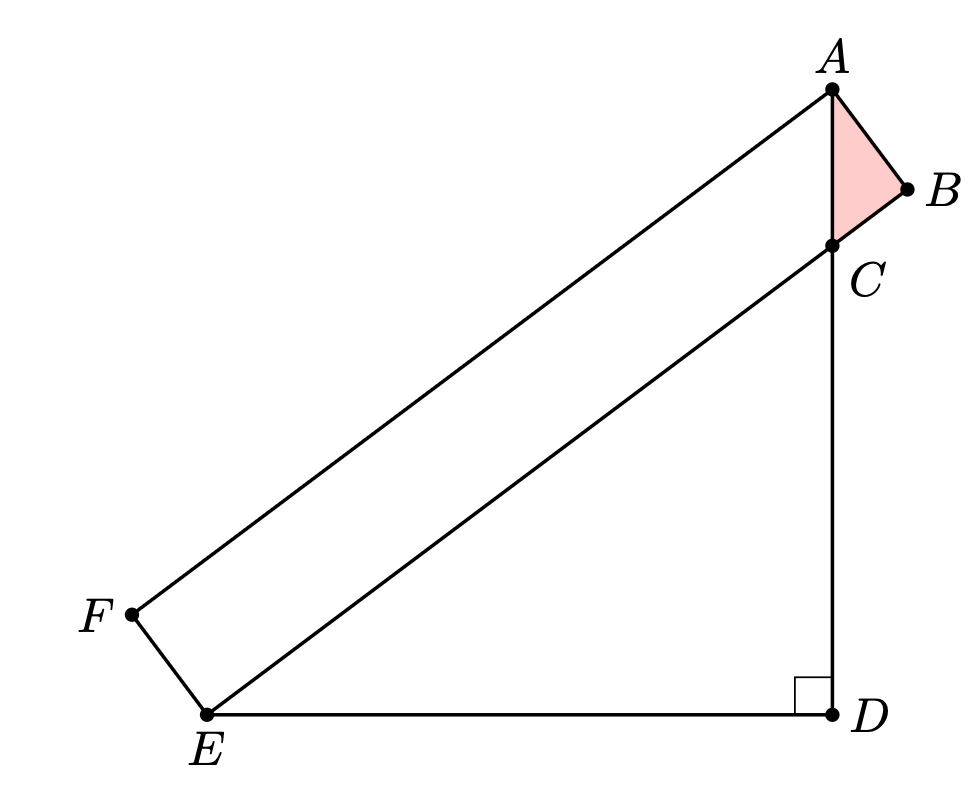
In the figure below, ABEF is a rectangle, \overline { A D } \bot \overline { D E }, A F = 7, A B = 1, and A D = 5.

What is the area of \triangle{ABC}?

  • A.

    \frac { 3 } { 8 }

  • B.

    \frac { 4 } { 9 }

  • C.

    \frac { 1 } { 8 }\sqrt { 1 3 }

  • D.

    \frac { 7 } { 1 5 }

  • E.

    \frac { 1 } { 8 } \sqrt { 1 5 }

Answer:A

 

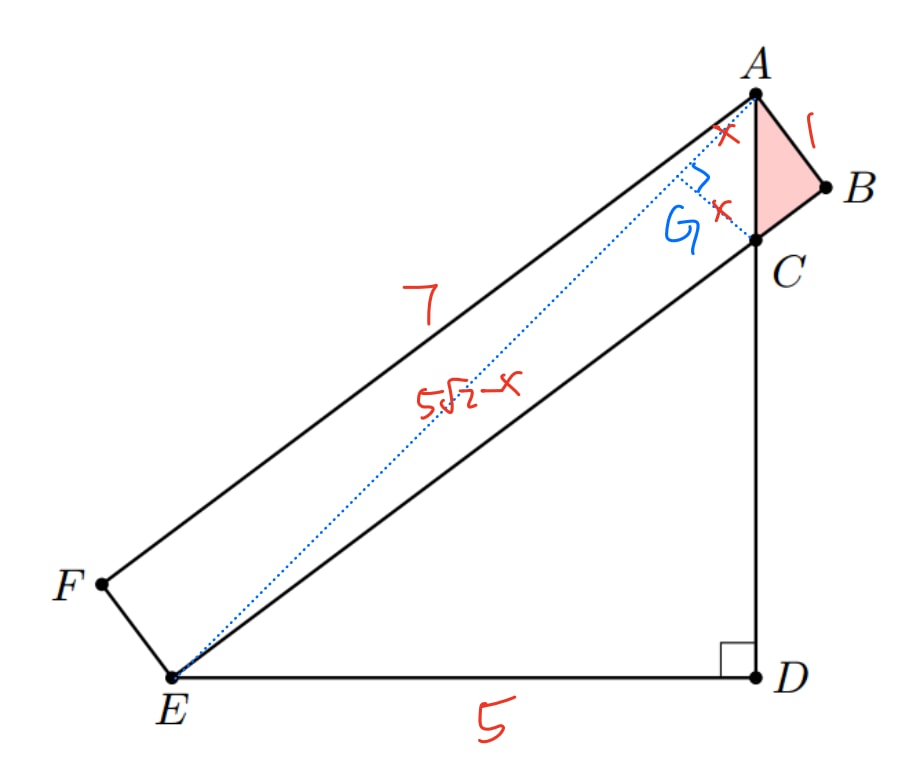
By Pythagorean theorem, we can see that AE=5\sqrt{2}, DE=5. So \triangle ADE is a right isoceles triangle, \angle EAD = 45^\circ.

Make altitude CG\perp AE at G. Set CG=AG=x, then EG=5\sqrt{2}-x. As \triangle ECG \sim \triangle EAB, \dfrac{EG}{GC}=\dfrac{5\sqrt{2}-x}{x}=\dfrac{EB}{BA}=7

So x=\dfrac{5\sqrt{2}}{8}. Area calculation: S_{\triangle ABC}= S_{\triangle ABE} - S_{\triangle ACE} = \frac{1}{2} AB \cdot BE - \frac{1}{2} AE \cdot CG = \frac{3}{8}.

Related Problems
Problem 13 2025 AMC 10 A
Problem 14 2025 AMC 10 A
Problem 16 2025 AMC 10 A
Problem 17 2025 AMC 10 A
Think Academy Powered by ChatGPT