2022 AMC 8

Complete problem set with solutions and individual problem pages

Problem 24 Hard

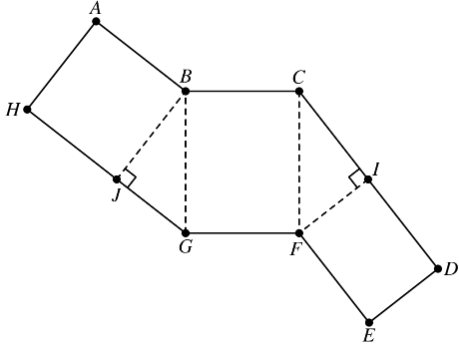
The figure below shows a polygon ABCDEFGH, consisting of rectangles and right triangles. When cut out and folded on the dotted lines, the polygon forms a triangular prism. Suppose that AH = EF = 8 and GH = 14. What is the volume of the prism?

  • A.

    112

  • B.

    128

  • C.

    192

  • D.

    240

  • E.

    288

Answer:C

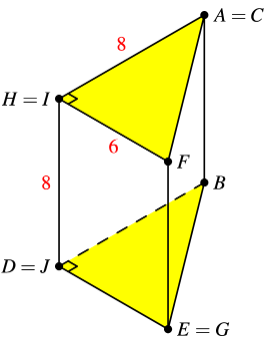
While imagining the folding, \overline{AB} goes on \overline{BC}, \overline{AH} goes on \overline{CI}, and \overline{EF} goes on \overline{FG}. So, BJ=CI=8 and FG=BC=8. Also, \overline{HJ} becomes an edge parallel to \overline{FG}, so that means HJ=8.

Since GH=14, then JG=14-8=6. So, the area of \triangle BJG is \frac{8\cdot6}{2}=24. If we let \triangle BJG be the base, then the height is FG=8. So, the volume is 24\cdot8=\boxed{\textbf{(C)} ~192}.

 

Remark

After folding polygon ABCDEFGH on the dotted lines, we obtain the following triangular prism:

Related Problems
Problem 21 2022 AMC 8
Problem 22 2022 AMC 8
Problem 23 2022 AMC 8
Problem 25 2022 AMC 8
Think Academy Powered by ChatGPT