2025 AMC 10 A

Complete problem set with solutions and individual problem pages

Problem 19 Easy

 

 

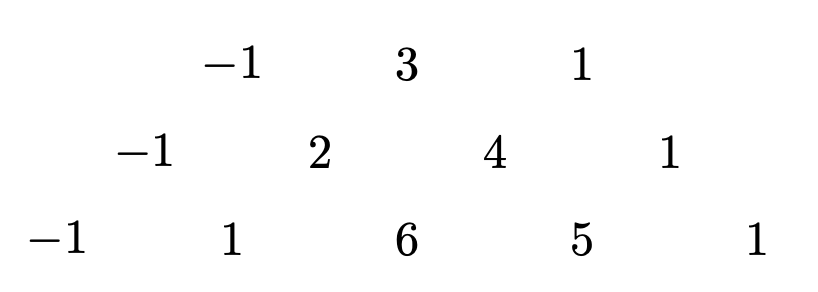
  • A.

    -29

  • B.

    -21

  • C.

    -14

  • D.

    -8

  • E.

    -3

Answer:A

Let S_n represent the sum of row n. Since all the numbers in row n+1 can be seen as the sum of the two numbers above it (one number above for the leftmost -1 and rightmost 1), we have the recurrence relation S_{n+1} = 2S_n, yielding S_n = 3 \times 2^{n-1}. As 12288=3 \times 2^{12}, it is the sum of the 13-th row.

Define a_n as the second element of row n, and b_n as the third element.

From the pattern: a_{n+1} = a_n - 1 with a_1 = 3, which gives a_n = 4 - n for n \geq 1.

With b_n = b_{n-1} + a_{n-1} and b_1 = 1: b_n - b_1 = \sum_{k=2}^{n} a_{k-1} = \sum_{k=1}^{n-1} a_k = \sum_{k=1}^{n-1} (4-k) = 4(n-1) - \frac{n(n-1)}{2}

Therefore, b_n = 4n - 3 - \frac{n(n-1)}{2}. b_{13} = 4 \times 13 - 3 - \frac{13 \times 12}{2} = -29

Related Problems
Problem 17 2025 AMC 10 A
Problem 18 2025 AMC 10 A
Problem 20 2025 AMC 10 A
Problem 21 2025 AMC 10 A
Think Academy Powered by ChatGPT