AMC 8 Daily Practice - Solid Figures

Complete problem set with solutions and individual problem pages

Problem 4 Easy

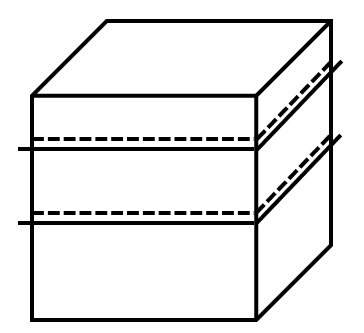
A cube is cut by two planes parallel to its base, dividing it into three rectangular prisms. The ratio of the surface areas of these three prisms is 3:4:5. What is the ratio of their volumes?

  • A.

    3:4:5

  • B.

    3:8:13

  • C.

    3:4:8

  • D.

    1:3:4

  • E.

    5:8:13

Answer:B

As shown in the figure, let the edge length of the cube be 1, and let the heights of the three rectangular prisms be x, y, and z respectively.

Thus, we have: x + y + z = 1.

The surface area of each rectangular prism includes the two base areas (each equal to 1 \times 1 = 1) and the lateral surface area (equal to 4 \times \text{height} since the base is a unit square).

Therefore, the surface areas of the three prisms are 2 + 4x, 2 + 4y, and 2 + 4z respectively.

Given their ratio is 3:4:5, we have: (2 + 4x) : (2 + 4y) : (2 + 4z) = 3 : 4 : 5.

Solving this proportion, we find: x = \frac{1}{8}, \quad y = \frac{1}{3}, \quad z = \frac{13}{24}.

Since the volumes of the prisms (with the same base area) are proportional to their heights, the ratio of their volumes is equal to the ratio of their heights: x : y : z = \frac{1}{8} : \frac{1}{3} : \frac{13}{24} = 3 : 8 : 13.

Related Problems
Problem 2 AMC 8 Daily Practice - Solid Figures
Problem 3 AMC 8 Daily Practice - Solid Figures
Problem 5 AMC 8 Daily Practice - Solid Figures
Problem 6 AMC 8 Daily Practice - Solid Figures
Think Academy Powered by ChatGPT