2025 AMC 10 A

Complete problem set with solutions and individual problem pages

Problem 10 Easy

A semicircle has diameter \overline {AB} and chord \overline {CD} of length 16 parallel to \overline {AB}. A smaller semicircle with diameter on \overline {AB} and tangent to \overline {CD} is cut from the larger semicircle, as shown below.

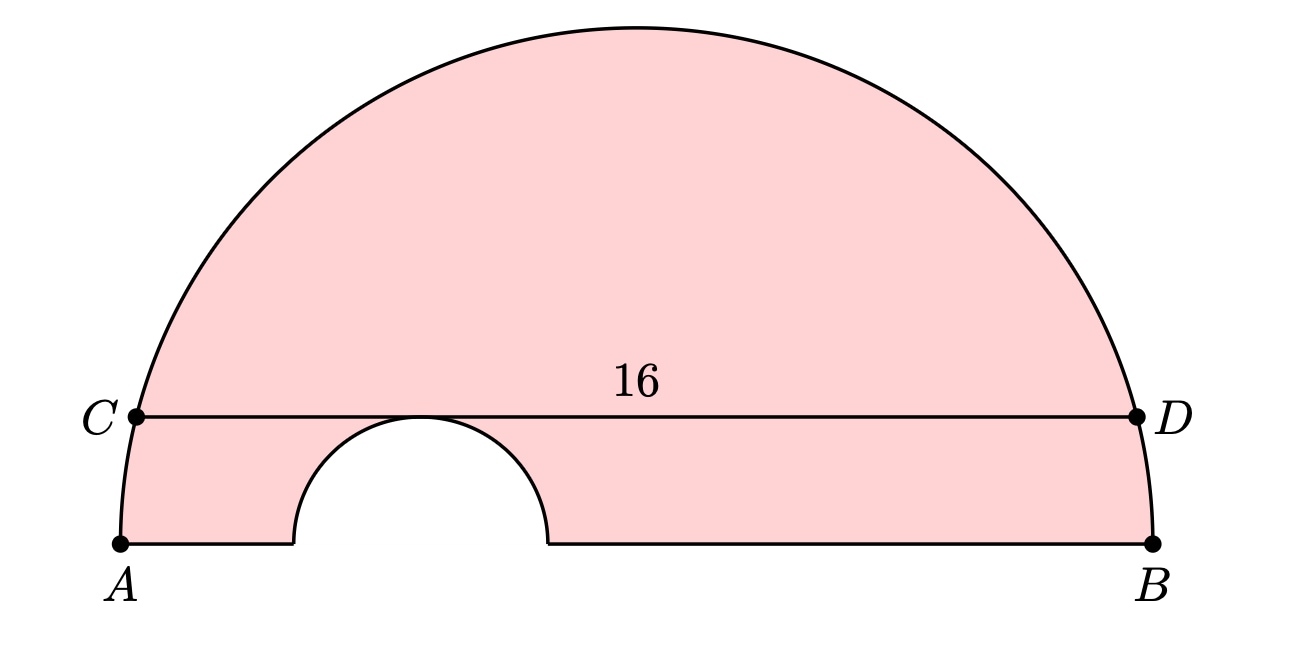
What is the area of the resulting figure, shown shaded?

  • A.

    16\pi

  • B.

    24\pi

  • C.

    32\pi

  • D.

    48\pi

  • E.

    64\pi

Answer:C

 

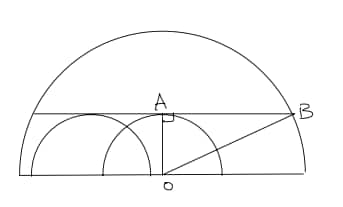
Let r and R denote the radii of the smaller and larger semicircles respectively.

As in the diagram, we can translate the tangent smaller semi-circle to be centered at O. So OB = R, OA = r, and AB=16/2=8. Thus R^2-r^2 = 8^2.

The answer is: \frac{1}{2}\pi R^2 - \frac{1}{2}\pi r^2 = \frac{1}{2}\pi(R^2 - r^2) = \frac{1}{2}\pi \times 64 = 32\pi

Related Problems
Problem 8 2025 AMC 10 A
Problem 9 2025 AMC 10 A
Problem 11 2025 AMC 10 A
Problem 12 2025 AMC 10 A
Think Academy Powered by ChatGPT