2025 AMC 8
Complete problem set with solutions and individual problem pages
A classroom has a row of 35 coat hooks. Paulina likes coats to be equally spaced, so that there is the same number of empty hooks before the first coat, after the last coat, and between every coat and the next one. Suppose there is at least 1 coat and at least 1 empty hook. How many different numbers of coats can satisfy Paulina's pattern?
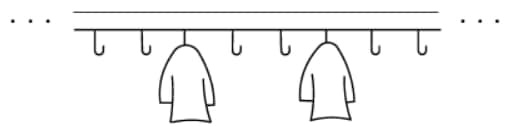
- A.
- B.
- C.
- D.
- E.
Solution 1
Suppose there are coats on the rack. Notice that there are "gaps" formed by these coats, each of which must have the same number of empty spaces (say, ). Then the values and must satisfy . We now use Simon's Favorite Factoring Trick as follows:
Our only restrictions now are that and . Other than that, each factor pair of produces a valid solution , which in turn uniquely determines an arrangement. Since has factors, our answer is .
Solution 2
Say Paulina placed coats. That will divide the 35 hooks into spaces and empty hooks. Therefore,The values of that satisfy this areThe answer is .
