2021 AMC 10 A Fall

Complete problem set with solutions and individual problem pages

Problem 22 Hard

Inside a right circular cone with base radius 5 and height 12 are three congruent spheres with radius r. Each sphere is tangent to the other two spheres and also tangent to the base and side of the cone. What is r ?(2021 AMC Fall 10A, Question #22)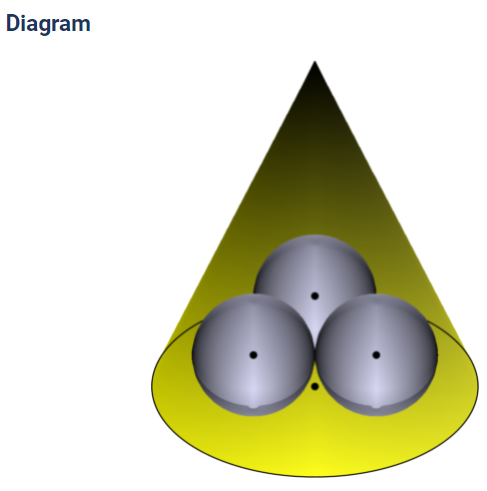

  • A.

    \frac{3}{2}

  • B.

    \frac{90-40 \sqrt{3}}{11}

  • C.

    2

  • D.

    \frac{144-25 \sqrt{3}}{44}

  • E.

    \frac{5}{2}

Answer:B

Solution 1:

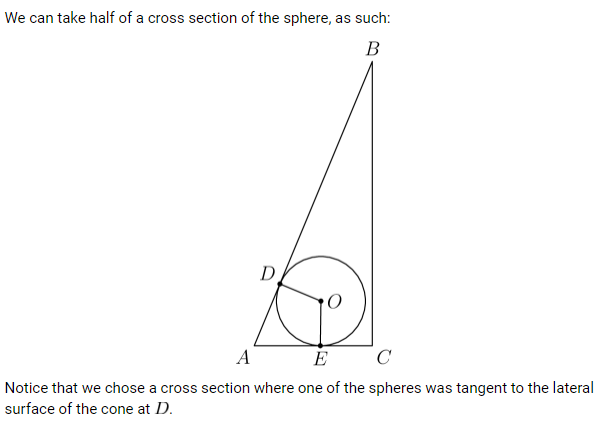
Notice that we chose a cross section where one of the spheres was tangent to the lateral surface of the cone at D. To evaluate r, we will find A E and E C in terms of r; we also know that A E+E C=5, so with this, we can solve r. Firstly, to find E C, we can take a bird's eye view of the cone: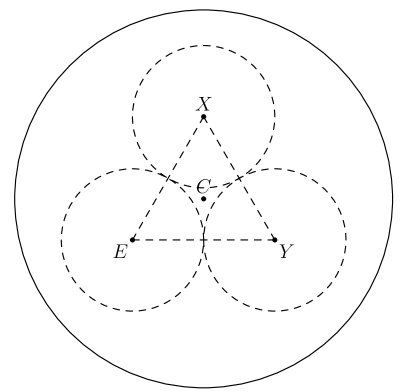

Note that C is the centroid of equilateral triangle E X Y. Also, since all of the medians of an equilateral triangle are also altitudes, we want to find two-thirds of the altitude from E to X Y; this is because medians cut each other into a 2 to 1 ratio. This equilateral triangle has a side length of 2 r, therefore it has an altitude of length r \sqrt{3}; two thirds of this is \frac{2 r \sqrt{3}}{3}, so E C=\frac{2 r \sqrt{3}}{3}

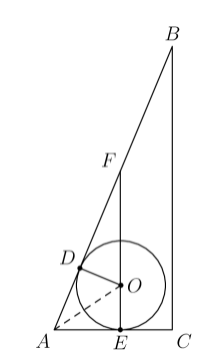
To evaluate A E in terms of r, we will extend \overline{O E} past point O to \overline{A B} at point F . \triangle A E F is similar to \triangle A C B. Also, A O is the angle bisector of \angle E A B. Therefore, by the angle bisector theorem, \frac{O E}{O F}=\frac{A E}{A F}=\frac{5}{13}. Also, O E=r, so \frac{r}{O F}=\frac{5}{13}, so O F=\frac{13 r}{5}. This means that A E=\frac{5 \cdot E F}{12}=\frac{5 \cdot(O E+O F)}{12}=\frac{5 \cdot\left(r+\frac{13 r}{5}\right)}{12}=\frac{18 r}{12}=\frac{3 r}{2} We have that E C=\frac{2 r \sqrt{3}}{3} and that A E=\frac{3 r}{2}, so A C=E C+A E=\frac{2 r \sqrt{3}}{3}+\frac{3 r}{2}=\frac{4 r \sqrt{3}+9 r}{6}. We also were given that A C=5. Therefore, we have \frac{4 r \sqrt{3}+9 r}{6}=5 . This is a simple linear equation in terms of r. We can solve for r to get r=(\mathbf{B}) \frac{90-40 \sqrt{3}}{11} \text {. }

Solution 2:

We will use coordinates. WLOG, let the coordinates of the center of the base of the cone be the origin. Then, let the center of one of the spheres be \left(0, \frac{2 r}{\sqrt{3}}, r\right). Note that the distance between this point and the plane given by 12 y+5 z=60 is r. Thus, by the point-to-plane distance formula, we have \frac{\left|12 \cdot \frac{2 r}{\sqrt{3}}+5 r-60\right|}{\sqrt{0^{2}+5^{2}+12^{2}}}=r . Solving for r yields r= (B) \frac{90-40 \sqrt{3}}{11}

Related Problems
Problem 20 2021 AMC 10 A Fall
Problem 21 2021 AMC 10 A Fall
Problem 23 2021 AMC 10 A Fall
Problem 24 2021 AMC 10 A Fall
Think Academy Powered by ChatGPT