2025 AMC 10 A

Complete problem set with solutions and individual problem pages

Problem 9 Easy

Let f ( x ) = 1 0 0 x ^ { 3 } - 3 0 0 x ^ { 2 } + 2 0 0 x. For how many real numbers a does the graph of y=f(x-a) pass through the point (1,25)?

  • A.

    1

  • B.

    2

  • C.

    3

  • D.

    4

  • E.

    more than 4

Answer:C

 

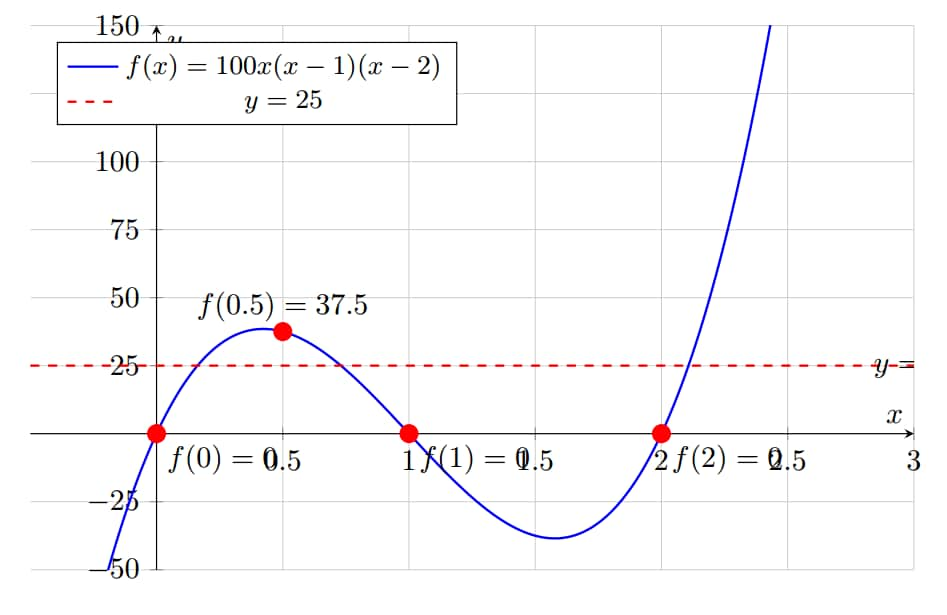
We seek the number of solutions of f(1-a)=25, which is equivalent to the number of solutions of f(x)=25.

Since f(x) = 100 \times x(x-1)(x-2), we have f(0) = f(1) = f(2) = 0. As the coefficient of x^3 is positive, we can draw the diagram of f(x).

Note that f\left(\frac{1}{2}\right) = 100 \times \frac{1}{2} \times \left(-\frac{1}{2}\right) \times \left(-\frac{3}{2}\right) = 25 \times \frac{3}{2} > 25

By the intermediate value theorem, there exist x_1 \in \left(0, \frac{1}{2}\right) and x_2 \in \left(\frac{1}{2}, 1\right) satisfying f(x_1) = f(x_2) = 25.

Since f(2) = 0 and f(3) > 100 > 25, there exists x_3 \in (2,3) with f(x_3) = 25.

As f(x) = 25 is a cubic equation with at most 3 real roots, x_1, x_2, x_3 are all the solutions.

Related Problems
Problem 7 2025 AMC 10 A
Problem 8 2025 AMC 10 A
Problem 10 2025 AMC 10 A
Problem 11 2025 AMC 10 A
Think Academy Powered by ChatGPT