2021 AMC 10 A Fall
Complete problem set with solutions and individual problem pages
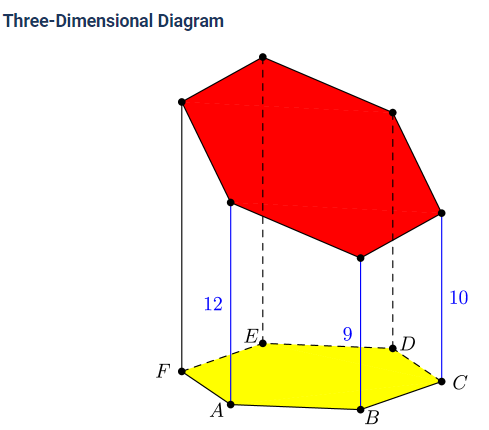
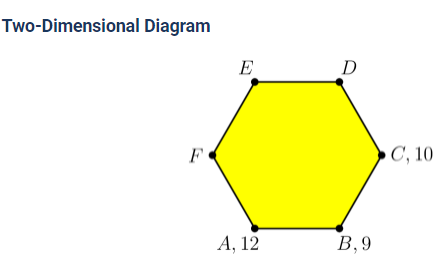
An architect is building a structure that will place vertical pillars at the vertices of regular hexagon , which is lying horizontally on the ground. The six pillars will hold up a flat solar panel that will not be parallel to the ground. The heights of pillars at , and are , and meters, respectively. What is the height, in meters, of the pillar at ?(2021 AMC Fall 10A, Question #17)
- A.
- B.
- C.
- D.
- E.
Solution 1:
The pillar at has height 9 and the pillar at has height 12 . Since the solar panel is flat, the inclination from pillar to pillar is 3 . Call the center of the hexagon . Since , it follows that the solar panel has height 13 at . Since the solar panel is flat, the heights of the solar panel at , and are collinear. Therefore, the pillar at has height
Solution 2:
Let the height of the pillar at be . Notice that the difference between the heights of pillar and pillar is equal to the difference between the heights of pillar and pillar . So, the height at is . Now, doing the same thing for pillar we get the height is . Therefore, we can see the difference between the heights at pillar and pillar is half the difference between the heights at and , so The answer is (D) 17 .
