AMC 10 Daily Practice - Tangency

Complete problem set with solutions and individual problem pages

Problem 1 Medium

As shown in the figure, AC is a tangent to circle \odot O, and B is the point of tangency. Connect OA and OC. If m\angle A = 30^\circ, AB = 2\sqrt{3}, and BC = 3, then what is the length of OC?

 

 

  • A.

    3

  • B.

    2\sqrt{3}

  • C.

    \sqrt{13}

  • D.

    6

  • E.

    4

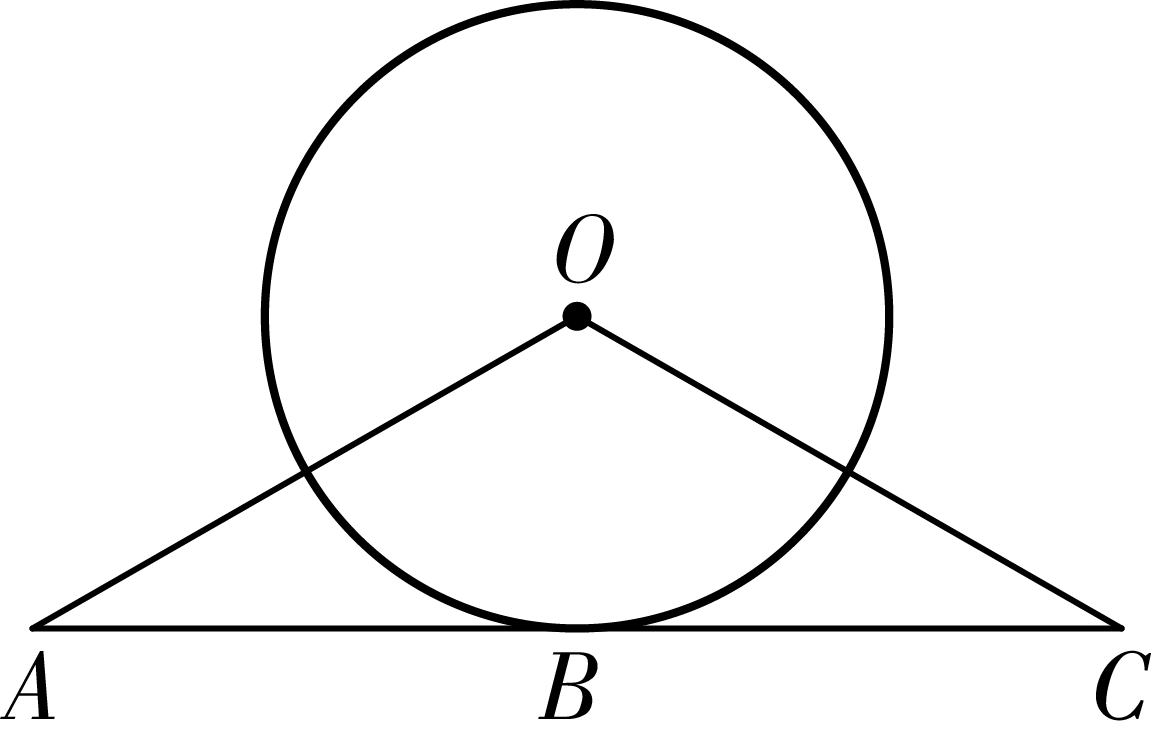
Answer:C

Connect OB

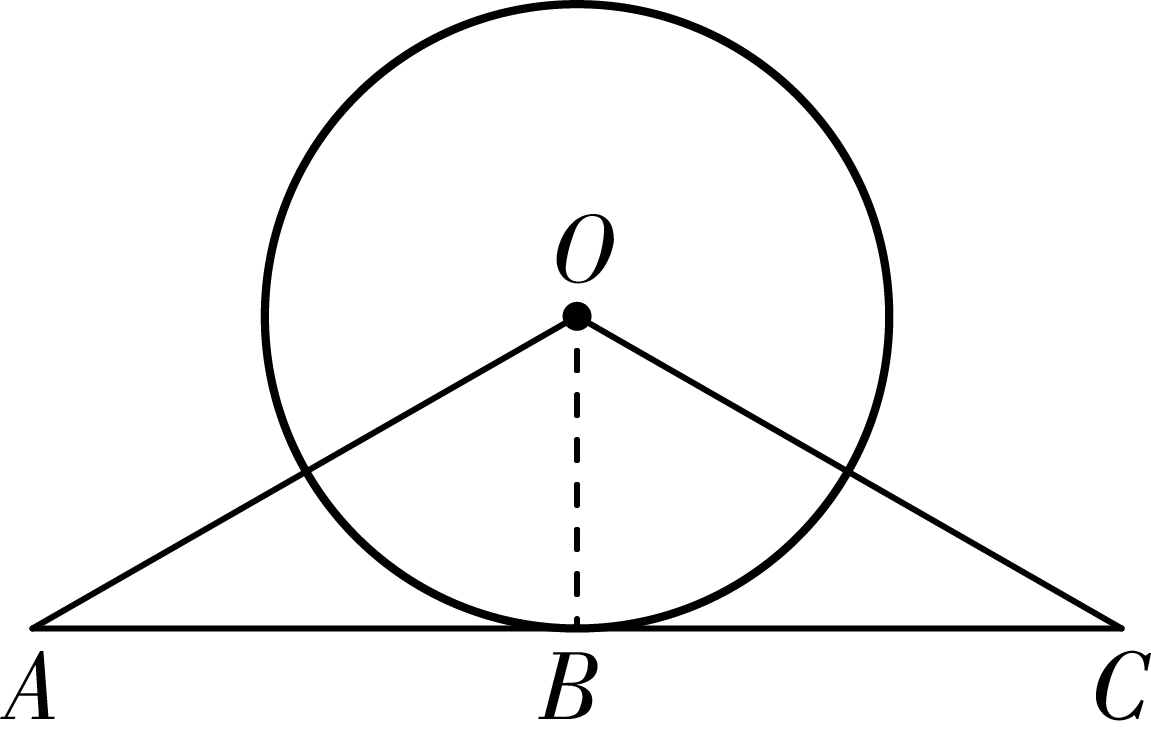
\because AC is tangent to circle \odot O, point B is the tangent point，

\therefore \overline{OB}\bot \overline{AC},

\because m\angle A=30{}^\circ, AB=2\sqrt{3},

\therefore In \text{Rt}\triangle OAB, OB=2\sqrt{3}\times \frac{\sqrt{3}}{3}=2,

\because BC=3,

\therefore In \text{Rt}\triangle OBC, OC=\sqrt{O{{B}^{2}}+B{{C}^{2}}}=\sqrt{13},

choose \text{C}.

Related Problems
Problem 2 AMC 10 Daily Practice - Tangency
Problem 3 AMC 10 Daily Practice - Tangency
Think Academy Powered by ChatGPT