2020 AMC 8
Complete problem set with solutions and individual problem pages
When a positive integer is fed into a machine, the output is a number calculated according to the rule shown below.
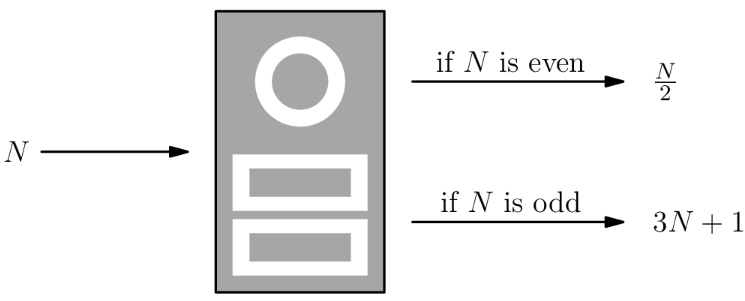
For example, starting with an input of the machine will output Then if the output is repeatedly inserted into the machine five more times, the final output is
When the same -step process is applied to a different starting value of the final output is What is the sum of all such integers
- A.
- B.
- C.
- D.
- E.
We start with final output of and work backward, taking cares to consider all possible inputs that could have resulted in any particular output. This produces following set of possibilities each stage:
where, for example, must come from (as there is no integer satisfying ), but could come from or (as , and is even while is odd). By construction, last set in this sequence contains all the numbers which will lead to number to end of the -step process, and sum is .
