2017 AMC 8

Complete problem set with solutions and individual problem pages

Problem 18 Hard

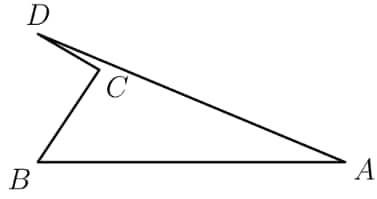
In the non-convex quadrilateral ABCD shown below, \angle BCD is a right angle, AB=12, BC=4, CD=3, and AD=13. What is the area of quadrilateral ABCD?

  • A.

    12

  • B.

    24

  • C.

    26

  • D.

    30

  • E.

    36

Answer:B

Solution 1

We first connect point B with point D.

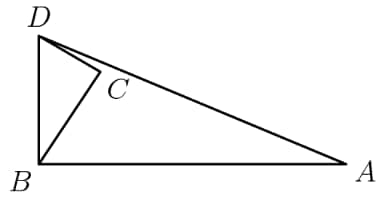
We can see that \triangle BCD is a 3-4-5 right triangle. We can also see that \triangle BDA is a right triangle, by the 5-12-13 Pythagorean triple. With these lengths, we can solve the problem. The area of \triangle BDA is \frac{5\cdot 12}{2}, and the area of \triangle BCD is \frac{3\cdot 4}{2}. Thus, the area of quadrilateral ABCD is 30-6 = \boxed{\textbf{(B)}\ 24}.

 

Solution 2

\triangle BCD is a 3-4-5 right triangle. So the area of \triangle BCD is 6. Then we can use Heron's formula to compute the area of \triangle ABD whose sides have lengths 5, 12, and 13. The area of \triangle ABD = \sqrt{s(s-5)(s-12)(s-13)} , where s is the semi-perimeter of the triangle, that is s=(5+12+13)/2=15. Thus, the area of \triangle ABD is 30, so the area of ABCD is 30-6 = \boxed{\textbf{(B)}\ 24}.

Related Problems
Problem 16 2017 AMC 8
Problem 17 2017 AMC 8
Problem 19 2017 AMC 8
Problem 20 2017 AMC 8
Think Academy Powered by ChatGPT