2021 AMC 10 B Fall
Complete problem set with solutions and individual problem pages
Three identical square sheets of paper each with side length 6 are stacked on top of each other. The middle sheet is rotated clockwise about its center and the top sheet is rotated clockwise about its center, resulting in the -sided polygon shown in the figure below. The area of this polygon can be expressed in the form , where , and are positive integers, and is not divisible by the square of any prime. What is ?(2021 AMC Fall 10B, Question #18)
- A.
- B.
- C.
- D.
- E.
Solution 1:
First note the useful fact that if is the circumradius of a dodecagon (12-gon) the area of the figure is . If we connect the vertices of the 3 squares we get a dodecagon. The radius of circumcircle of the dodecagon is simply half the diagonal of the square, which is . Thus the area of the dodecagon is . But, the problem asks for the area of figure of rotated squares. This area is the area of the dodecagon, which was found, subtracting the 12 isosceles triangles, which are formed when connecting the vertices of the squares to created the dodecagon. To find this area, we need to know the base of the isosceles triangle, call this . Then, we can use Law of Cosines, on the triangle that is formed from the two vertices of the square and the center of the square. After computing, we get that . Realize that the 12 isosceles are congruent with an angle measure of , this means that we can create 4 congruent equilateral triangles with side length of . The area of the equilateral triangle is . Thus, the area of all the twelve small equilateral traingles are . Thus, the requested area is . Thus, . Thus, the answer is (E)147.
Solution 2:
As shown in Image:2021_AMC_12B_(Nov)_Problem_15,_sol.png,
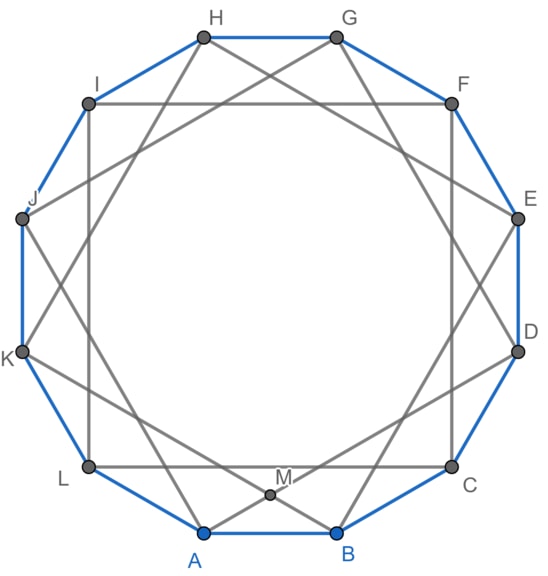
all 12 vertices of three squares form a regular dodecagon (12-gon). Denote by the center of this dodecagon. Hence, . Because the length of a side of a square is . Hence, . We notice that . Hence, . Therefore, the area of the region that three squares cover is Therefore, the answer is (E) 147 .
