2025 AMC 10 A

Complete problem set with solutions and individual problem pages

Problem 20 Easy

A silo (right circular cylinder) with diameter 20 meters stands in a field. MacDonald is located 20 meters west and 15 meters south of the center of the silo. McGregor is located 20 meters east and g>0 meters south of the center of the silo. The line of sight between MacDonald and McGregor is tangent to the silo. The value of g can be written as \frac { a \sqrt { b }-c } { d }, where a, b, c and d are positive integers, b is not divisible by the square of any prime, and d is relatively prime to the greatest common divisor of a and c. What is a+b+c+d?

  • A.

    119

  • B.

    120

  • C.

    121

  • D.

    122

  • E.

    123

Answer:A

 

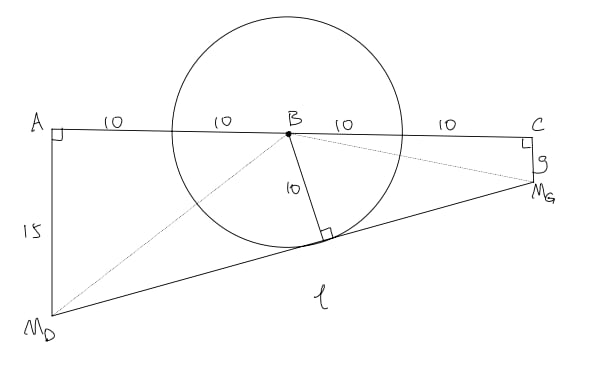
Let \ell denote the distance between points M_D and M_G. The trapezoid's area is: S_{\triangle BAM_D} + S_{\triangle BCM_G} + S_{\triangle BM_D M_G} = \frac{1}{2}(15 \times 20 + 20 \times 8 + 10 \times \ell)

Also, trapezoid area = \frac{1}{2}(15 + 8) \times 40.

Equating: \frac{1}{2}(300 + 20g + 10\ell) = \frac{1}{2}(15 + g) \times 40 gives \ell = 2g + 30.

Using the Pythagorean theorem: (2g + 30)^2 = 40^2 + (15 - g)^2.

Expanding: 4g^2 + 120g + 900 = 1600 + 225 - 30g + g^2

This simplifies to 3g^2 + 150g - 925 = 0.

Applying the quadratic formula: \Delta = 150^2 + 4 \times 3 \times 925 = 33600 g = \frac{-150 \pm \sqrt{33600}}{6} = \frac{-75 \pm 20\sqrt{21}}{3}

Since g > 0: g = \frac{-75 + 20\sqrt{21}}{3}.

Related Problems
Problem 18 2025 AMC 10 A
Problem 19 2025 AMC 10 A
Problem 21 2025 AMC 10 A
Problem 22 2025 AMC 10 A
Think Academy Powered by ChatGPT