2020 AMC 8
Complete problem set with solutions and individual problem pages
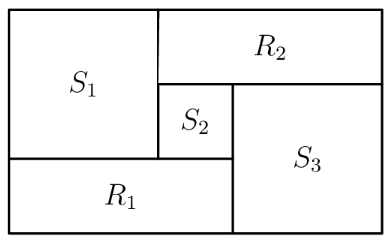
Rectangles and and squares and shown below, combine to form a rectangle that is 3322 units wide and 2020 units high. What is the side length of in units?
- A.
- B.
- C.
- D.
- E.
Solution 1
Let the side length of each square be . Then, from the diagram, we can line up the top horizontal lengths of , , and to cover the top side of the large rectangle, so . Similarly, the short side of will be , and lining this up with the left side of to cover the vertical side of the large rectangle gives . We subtract the second equation from the first to obtain , and thus .
Solution 2
Assuming that the problem is well-posed, it should be true in the particular case where and . Let the sum of the side lengths of and be , and let the length of square be . We then have the system
which we solve to determine .
